NDSolve`FEM`
NDSolve`FEM`

HexahedronElement

HexahedronElement[{{i11,…,i18},…,{in1,…,in8}}]

represents n linear hexahedron elements ek with incidents {ik1,…ik8}.

HexahedronElement[{{i11,…,i120},…,{in1,…,in20}}]

represents n quadratic hexahedron elements ek with incidents {ik1,…,ik20}.

HexahedronElement[{e1,…,en},{m1,…,mn}]

represents n hexahedron elements ek and n integer markers mk.

Details and Options

  • HexahedronElement is used to represent hexahedron mesh elements in ElementMesh.
  • HexahedronElement can be used as an input to ToElementMesh or ToBoundaryMesh.
  • Incidents ik,j are integers that index an array of spatial coordinates. The coordinates referenced by ek={ik1,…} are the nodes of the k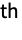^(th) triangle.
  • The first three incidents ik1 until ik8 are always vertices.
  • For quadratic triangle elements, the next 12 incidents are mid-side nodes of possibly curved edges.
  • Linear elements are order 1 elements and quadratic elements are order 2 elements.
  • In HexahedronElement[{e1,…,en}], all elements ek need to be of the same order.
  • The hexahedra in HexahedronElement[{e1,…,en}] will share common nodes, edges, and faces, but cannot intersect with each other or with themselves.
  • The nodes for a linear and a quadratic hexahedron are shown:
  • For a HexahedronElement, the incidents on the faces must be counterclockwise when viewed from inside the element. An element {i1,…,i8} has face incidents {i1,i2,i3,i4}, {i8,i7,i6,i5}, {i1,i5,i6,i2}, {i2,i6,i7,i3}, {i3,i7,i8,i4}, and {i4,i8,i5,i1} for the six faces.
  • The hexahedron element is known in the finite element method as a Serendipity element.

Examples

open allclose all

Basic Examples  (1)

Load the package:

Create a mesh with one quad element:

Generalizations & Extensions  (4)

The base coordinates of the linear element:

The base incidents of the linear element:

A mesh with a linear unit element:

Visualization of the linear unit element:

The base coordinates of the quadratic element:

The base incidents of the quadratic element:

The base face incidents of the linear element:

The base face incidents of the quadratic element:

Applications  (1)

A linear hexahedron element mesh with markers:

Visualizing the index of the coordinates at their respective positions:

Create the mesh:

Visualize the mesh with the element markers:

Possible Issues  (6)

The incidents must be of the appropriate length:

The incidents order cannot be mixed:

The incidents must be lists of integers:

The number of markers must match the number of incidents:

Markers must be a vector of integers:

When possible, noninteger markers will be converted to integers:

Wolfram Research (2014), HexahedronElement, Wolfram Language function, https://reference.wolfram.com/language/FEMDocumentation/ref/HexahedronElement.html.

Text

Wolfram Research (2014), HexahedronElement, Wolfram Language function, https://reference.wolfram.com/language/FEMDocumentation/ref/HexahedronElement.html.

CMS

Wolfram Language. 2014. "HexahedronElement." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/FEMDocumentation/ref/HexahedronElement.html.

APA

Wolfram Language. (2014). HexahedronElement. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/HexahedronElement.html

BibTeX

@misc{reference.wolfram_2024_hexahedronelement, author="Wolfram Research", title="{HexahedronElement}", year="2014", howpublished="\url{https://reference.wolfram.com/language/FEMDocumentation/ref/HexahedronElement.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hexahedronelement, organization={Wolfram Research}, title={HexahedronElement}, year={2014}, url={https://reference.wolfram.com/language/FEMDocumentation/ref/HexahedronElement.html}, note=[Accessed: 22-December-2024 ]}