NDSolve`FEM`
NDSolve`FEM`

TetrahedronElement

TetrahedronElement[{{i11,i12,i13,i14},…,{in1,in2,in3,in4}}]

represents n linear tetrahedron elements ek with incidents {ik1,ik2,ik3,ik4}.

TetrahedronElement[{{i11,…,i110},…,{in1,…,in10}}]

represents n quadratic tetrahedron elements ek with incidents {ik1,…,ik10}.

TetrahedronElement[{e1,…,en},{m1,…,mn}]

represents n tetrahedron elements ek and n integer markers mk.

Details and Options

  • TetrahedronElement is used to represent tetrahedron mesh elements in ElementMesh.
  • TetrahedronElement can be used as an input to ToElementMesh.
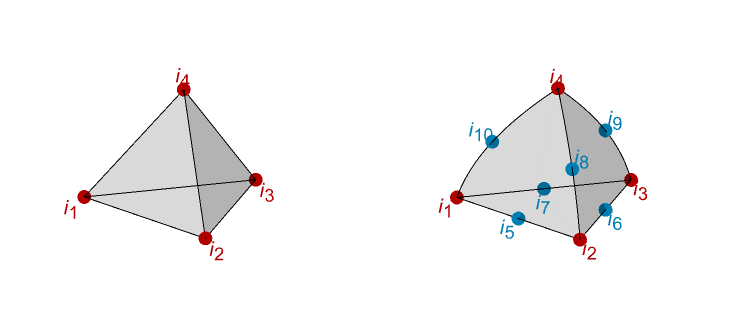
  • Incidents ik,j are integers that index an array of spatial coordinates. The coordinates referenced by ek={ik1,…} are the nodes of the k^(th) tetrahedron.
  • The first four incidents ik1, ik2, ik3, and ik4 are always vertices.
  • For quadratic tetrahedron elements, the next six incidents are mid-side nodes of possibly curved edges.
  • Linear elements are order 1 elements and quadratic elements are order 2 elements.
  • In TetrahedronElement[{e1,…,en}], all elements ek need to be of the same order.
  • The tetrahedra in TetrahedronElement[{e1,…,en}] will share common nodes, edges, and faces but cannot intersect with each other, or for second-order tetrahedra, with themselves.
  • The nodes for a linear and a quadratic tetrahedra are shown:
  • For a TetrahedronElement, the face incidents opposite a vertex ij must be counterclockwise. An element {i1,i2,i3,i4} has the face incidents {i4,i3,i2}, {i4,i1,i3}, {i4,i2,i1}, and {i1,i2,i3} for the four faces.
  • The tetrahedron element is known in the finite element method as a Serendipity element.

Examples

open allclose all

Basic Examples  (1)

Load the package:

Create a mesh with one tetrahedron element:

Generalizations & Extensions  (4)

The base coordinates of the linear element:

The base incidents of the linear element:

A mesh with a linear unit element:

Visualization of the linear unit element:

The base coordinates of the quadratic element:

The base incidents of the quadratic element:

The base face incidents of the linear element:

The base face incidents of the quadratic element:

Applications  (1)

A set of linear tetrahedron elements mesh with markers:

Visualizing the index of the coordinates at their respective positions:

Create the mesh:

Visualize the mesh with the elements' markers:

Possible Issues  (6)

The incidents must be of the appropriate length:

The incident order cannot be mixed:

The incidents must be lists of integers:

The number of markers must match the number of incidents:

Markers must be a vector of integers:

When possible, noninteger markers will be converted to integers:

Wolfram Research (2014), TetrahedronElement, Wolfram Language function, https://reference.wolfram.com/language/FEMDocumentation/ref/TetrahedronElement.html.

Text

Wolfram Research (2014), TetrahedronElement, Wolfram Language function, https://reference.wolfram.com/language/FEMDocumentation/ref/TetrahedronElement.html.

CMS

Wolfram Language. 2014. "TetrahedronElement." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/FEMDocumentation/ref/TetrahedronElement.html.

APA

Wolfram Language. (2014). TetrahedronElement. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/TetrahedronElement.html

BibTeX

@misc{reference.wolfram_2024_tetrahedronelement, author="Wolfram Research", title="{TetrahedronElement}", year="2014", howpublished="\url{https://reference.wolfram.com/language/FEMDocumentation/ref/TetrahedronElement.html}", note=[Accessed: 04-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_tetrahedronelement, organization={Wolfram Research}, title={TetrahedronElement}, year={2014}, url={https://reference.wolfram.com/language/FEMDocumentation/ref/TetrahedronElement.html}, note=[Accessed: 04-November-2024 ]}