IPOPTを使った最適化

IPOPT (Interior Point OPTimizer)は，数理最適化問題の局所解を求めるために設計された，大規模非線形最適化のためのソフトウェアパッケージである．

IPOPTLink はWolfram LibraryLink を使ってIPOPT関数にリンクする，Wolframシステムのアプリケーションである．IPOPTLink はIPOPTMinimizeやParametricIPOPTMinimize等，さまざまな関数を提供する．これらの関数はパラメータを使って，または使わないで極小値を求めるのに使用できる．これらはWolfram言語のFindMinimum等の最適化関数で自動的に使用される．

しかし，IPOPTLink の関数を直接呼び出して，IPOPTに実装された機能をより柔軟に使用することもできる．

IPOPTLink の基本的な関数

IPOPTはの約条件付きの数学的な 次元制最適化問題の解を求めるように設計されている．条件付き最適化問題は，目的関数と呼ばれる，複数の変数の実数値の関数 を制約条件の下で極小化する問題である．制約条件として，変数を制約する条件か，関数で定義される制約条件の2種類を指定することができる．変数を制約する条件は， （ただし x=(x₁,…,x_n)）という形である．関数の制約条件は，という形である．

IPOPTMinimizeは，制約条件の種類によって，次の3つの方法で使用できる：

IPOPTMinimizeの使用法

目的関数の極大化は，関数の負数を極小化することで行える．

制約条件なしの極小化

制約条件なしの極小化IPOPTMinimize

IPOPTLink を使用するためには，パッケージをロードする必要がある．

最初の例では，から始めて，の極小値を求める．

IPOPTMinimizeを使ってIPOPTソルバを呼び出す．目的関数を ，引数変数を{}，初期値を{}とする．

x=10から始めて， を極小化する．

IPOPTMinimizeはIPOPTDataオブジェクトを返す．オブジェクトには極小値が含まれる．

IPOPTDataオブジェクトは，極小値が見付かった座標点も含んでいる．

境界の制約付き極小化

境界制約条件付き極小化IPOPTMinimize

x が区間 に制限された の極小値を，から始めて求める．ここでもIPOPTMinimizeを使い，目的関数を ，引数変数を ，初期値を とする．変数の境界も指定する必要がある：

x が10と20の間の値であるときに，x=11から始めて を極小化する．

IPOPTMinimizeはIPOPTDataオブジェクトを返す．オブジェクトには極小値と極小化点が含まれる．

境界の制約条件は，関数の制約条件の特殊な場合である．

制約条件付き関数の極小化

関数の制約条件と変数の境界による制約条件付き極小化IPOPTMinimize

を円上で極小化する．制約関数は であり，上下制約境界は1に等しい．

をにおいて，{x,y}={0,1}から始めて極小化する．

ParametricIPOPTMinimize

ParametricIPOPTMinimizeは問題設定において任意の場所にパラメータが存在する極小化問題を設定する際に使用できる．最適化問題はその後，異なるパラメータ値で繰り返し解くことができる．ParametricIPOPTMinimizeはIPOPTMinimizeの引数すべてに加え，最後にパラメータ変数引数{p₁,…}を取る．

制約条件付きのパラメトリックな極小化ParametricIPOPTMinimize

円（r はパラメータ）上で極小化問題を設定する．

を の下で，{x,y}={0,-r}から始めて極小化する．

このステップは関数の前処理とすべての必要な微分を行い，ParametricFunctionを返してパラメータ値を待機する．

実際の極小化はパラメータ値を与えた後に始まり，解はIPOPTData式に保存される．

異なるパラメータ値について，別の解を計算する．

複数のパラメータ値についてIPOPTMinimizeの代りにParametricIPOPTMinimizeを使うと，目的関数と制約関数の処理，および必要なすべての微分を繰り返すことによるオーバーヘッドを削減する．これは複雑さによっては大幅な削減となり得る．

IPOPTMinimizeを使った極大化

極大値は目的関数の負数を極小化することで求められる．

円上での極大値を求める．

の場合に，{x,y}={1,0}から始めて，を極大化する．

再び-f の極小値の負数を取っての極大値を求める．

の極大値と極大化点を抽出する：

工学における例

カムの曲率と半径に制約条件があるとき，凸面カムが1回転する際に，弁の開口面積を最大化するカムを設計する．問題設定はCOPSテストスイートからのものであり，以下にまとめる．

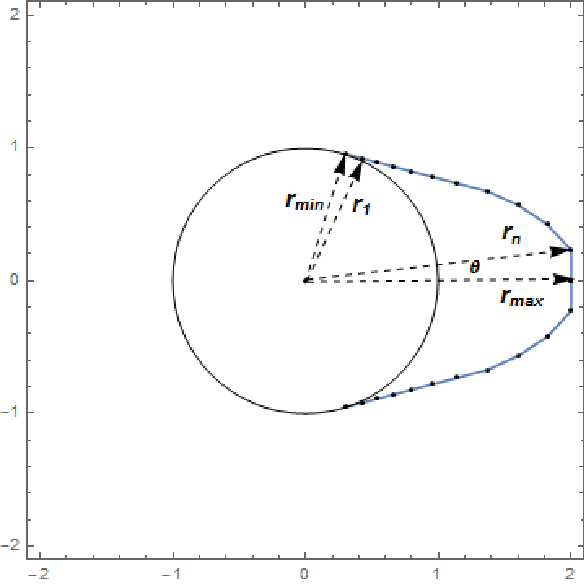
カムの形状は角度6π/5においては半径 r_min の円周であり，設計変数 r_i,i=1,…,n は，角度2π/5に均等に配分された角度 θ におけるカムの半径を表す．残りの角度2π/5は，これと対象となる．

以下の制約条件を指定する．各半径 r_i は区間{r_min, r_max}において制約される．また，A(r_i-1,r_i+1)≤A(r_i-1,r_i)+ A(r_i,r_i+1)で表される凸面の制約条件もある．ここでA(r_i,r_j)は原点とカム面の点 r_i， r_j で定義される三角形の面積である．さらにパラメータ α に依存する曲率についての条件-α ≤(r_i+1-r_i)/θ ≤α もある．

目的関数を定義するために，弁の開口面積と設計変数 r_i には π r_v ²(r₁+…+r_n)/n という単純な線形関係があると仮定する．ここで r_v は弁の形状に関連する定数である．

これは，パラメータ r_min，r_max， α のパラメトリックな問題として設定することができる．設計変数には n=20 を選び，と仮定する．

参考文献

IPOPTは​Andreas Wächter氏，​Carl Laird氏他によってCOIN-OR Initiativeの一環として書かれたものである．これは以下の論文に基づいている．A. Wächter and L. T. Biegler, 「​On the Implementation of a Primal-Dual Interior Point Filter Line Search Algorithm for Large-Scale Nonlinear Programming」，Mathematical Programming 106(1)，2006，pp. 25-57．