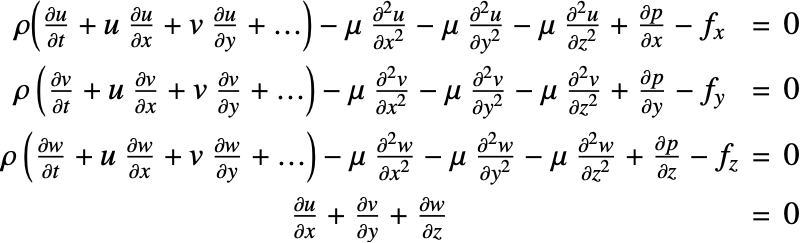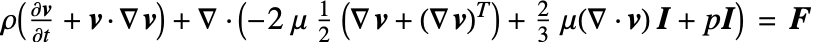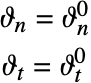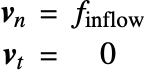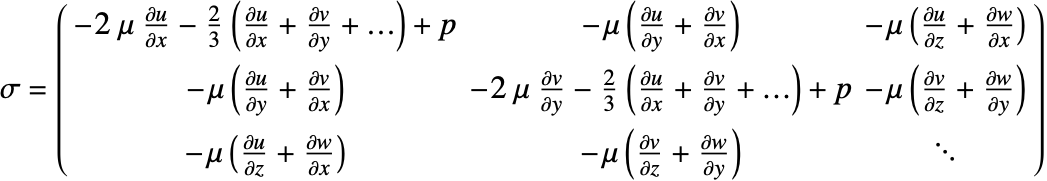Laminar Flow
Contents
Introduction
The analysis and behavior of fluids is of fundamental importance in science and engineering. This monograph gives an introduction to modeling fluids with partial differential equations. Equations and boundary conditions that are relevant for performing fluid mechanics analysis are derived and explained.
Fluids are substances in gaseous or liquid phase, like air or water, respectively. The term "fluid" comprises both liquids and gases. The opposite of fluids is solids, and the distinguishing attribute is that fluids cannot withstand shear stress when at rest. A fluid will take the shape of a container. The borderline between what is a fluid and a solid is not always clear. For example, asphalt is usually considered to be solid but on a longer timescale, it starts to behave as a fluid.
A distinction is typically made between the following fluid regimes:
The difference between these three flow regimes is given by the Reynolds number ![]() , which is the ratio of inertia forces versus viscous forces. It is used to predict whether or not turbulence will appear in a fluid flow. Turbulent flow is characterized by a high Reynolds number, while laminar flow occurs when the Reynolds number is small. The term creep flow is reserved for flows with a very small Reynolds number. The concept of the Reynolds number will be introduced more formally later and what high and low Reynolds number means will also be discussed.
, which is the ratio of inertia forces versus viscous forces. It is used to predict whether or not turbulence will appear in a fluid flow. Turbulent flow is characterized by a high Reynolds number, while laminar flow occurs when the Reynolds number is small. The term creep flow is reserved for flows with a very small Reynolds number. The concept of the Reynolds number will be introduced more formally later and what high and low Reynolds number means will also be discussed.
This monograph focuses on laminar flow.
Modeling fluids with partial differential equations (PDEs) is not the only way to model fluids. Other techniques include setting up ordinary differential equations (ODEs). This approach is followed by the Wolfram System Modeler. Roughly speaking, the system modeler approach is more suitable for large systems of flows interacting, like flow though pipes, while the partial differential equation approach is more suitable for a fine-grained analysis of a specific fluid flow behavior. In some cases, it is beneficial to use a combination of the two approaches.
The approach taken here is that in an introductory section, a single fluid flow example, a driven cavity example, is used to introduce various fluid flow analysis types and the functionality available. This will be followed by a more theoretical explanation of the underlying ideas and concepts. The theoretical background is much easier to understand once an intuition for the various analysis types exists. After that, the available boundary conditions are discussed.
The goal of a fluid flow analysis is to find the vector-valued fluid flow velocities of a fluid under constraints. Another goal might be to find the scalar pressure field or the scalar density field, depending on whether an incompressible or a compressible fluid is considered. The analysis and interpretation of the fluid behavior is useful to create a better-quality engineering design of the flow behavior in question. For example, through some parts of an object there might not be sufficient flow. These areas can then be identified and improved upon.
A fluid flow analysis is typically done in stages. First, for the body in which the fluid flows, a geometric model needs to be created. The geometric model is typically created within a computer-aided design (CAD) process. CAD models can either be imported or created in product. To import geometries, common file formats like DXF, STL or STEP are supported. These geometries can be imported with Import. The alternative is to create the geometrical models in product, for example, by using OpenCascadeLink. Once the geometric model is made available, some thought needs to be put into what type of analysis is to be performed. Currently supported analysis types are static and time-dependent fluid flow analysis. The next step is the setup of boundary conditions and constraints. Material properties of the fluid in question further specify the PDE model. Once the PDE model is fully specified, the subsequent finite element method will then compute the desired quantities under investigation. These quantities are then post-processed, either by visualizing them or some derived quantities are computed. This notebook shows the necessary steps for everything except the CAD model generation.
The modeling process as such results in a system of partial differential equations (PDEs) that can be solved with NDSolve and ParametricNDSolve.
Many of the animations of the simulation results shown in this tutorial are generated with a call to Rasterize. This is to reduce the disk space required. The downside is that the visual quality of the animations will not be as crisp as without it. To obtain high-quality graphics, remove or comment out the call to Rasterize.
The symbols and corresponding units used throughout this tutorial are summarized in the Nomenclature section.
Overview Example and Analysis Types
This monograph starts with an overview example, which focuses on the workflow more than the actual equations and theory. This example considers the flow of glycerol in a narrowing tube.
Creating a fluid flow model always comprises the same steps:
The dependent velocity variables ![]() ,
, ![]() represent the displacement in the
represent the displacement in the ![]() , and
, and ![]() directions, respectively.
directions, respectively. ![]() is the pressure.
is the pressure.
Here used chemical entity. Alternatively, it is also possible to specify material properties.
The inflow velocity in the ![]() direction is prescribed through boundary conditions. This is done by specifying an inflow profile for the
direction is prescribed through boundary conditions. This is done by specifying an inflow profile for the ![]() dependent variable on the left-hand side of the region. On the bottom and upper parts of the region, a wall boundary condition is specified. This is done by setting both the
dependent variable on the left-hand side of the region. On the bottom and upper parts of the region, a wall boundary condition is specified. This is done by setting both the ![]() and
and ![]() components on those parts to 0. An outflow condition is set on the right-hand side of the domain. Here the pressure
components on those parts to 0. An outflow condition is set on the right-hand side of the domain. Here the pressure ![]() is arbitrarily set to 0. In general, each dependent variable should either have a Dirichlet condition or a Robin-type Neumann specified. A pure Neumann value like Neumann 0 is not sufficient. In that case, the solution to the equation can only be correct up to a constant.
is arbitrarily set to 0. In general, each dependent variable should either have a Dirichlet condition or a Robin-type Neumann specified. A pure Neumann value like Neumann 0 is not sufficient. In that case, the solution to the equation can only be correct up to a constant.
A stable solution can be found if the velocities are interpolated with a higher order than the pressure. NDSolve allows an interpolation order for each dependent variable to be specified. Most of the time, specifying the "InterpolationOrder" is not necessary, but this is a standard procedure when using the finite element method for fluid flow and this is how it can be done in the Wolfram Language. This setup corresponds to what is called P2P1- or Q2Q1-type elements, which are also known as Taylor–Hood elements. Leaving out the "InterpolationOrder" will result in using a second-order interpolation for all variables, which can lead to instabilities.
In many cases, there is no need to generate a mesh; passing the geometry to the solver is sufficient.
This gives an overview of the workflow. The next sections describe the steps in more detail.
Stationary Analysis
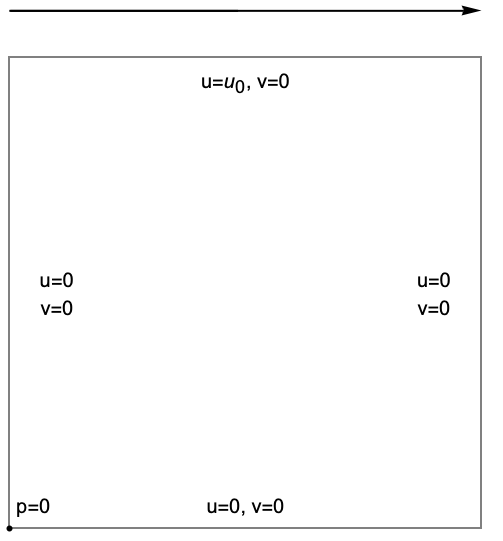
In this example, the driven cavity example, a classic benchmark in fluid dynamics [6] is investigated. Here a rectangular region is filled with a fluid. On the top there is a mechanism that drives the fluid with a fixed flow velocity in the positive ![]() direction, much like a conveyor belt would. The remaining sides are walls and have a no-slip condition. No-slip means that the velocity at the wall boundary is 0 in both the
direction, much like a conveyor belt would. The remaining sides are walls and have a no-slip condition. No-slip means that the velocity at the wall boundary is 0 in both the ![]() and
and ![]() directions. In the lower-left corner, there is a reference pressure condition.
directions. In the lower-left corner, there is a reference pressure condition.
In a rectangular region filled with a fluid, the top is driven by a velocity ![]() in the
in the ![]() direction. All other edges are walls, where a no-slip,
direction. All other edges are walls, where a no-slip, ![]() boundary condition is set.
boundary condition is set.
This driven cavity will be modeled as a time-independent, stationary, model. The dependent velocity variables ![]() and
and ![]() and the dependent pressure variable
and the dependent pressure variable ![]() are set up. The independent variables are the spatial variables
are set up. The independent variables are the spatial variables ![]() and
and ![]() .
.
Standard texts present this example with various Reynolds numbers ![]() . With everything else remaining the same, the flow pattern changes, depending only on the values of the Reynolds number
. With everything else remaining the same, the flow pattern changes, depending only on the values of the Reynolds number ![]() .
.
A reference pressure point should be applied in a "calm" area, or in other words, far away from the interesting behavior.
The solution returned constrains the ![]() velocity profile, which is the velocity profile in the
velocity profile, which is the velocity profile in the ![]() direction; the
direction; the ![]() velocity profile, which is the velocity profile in the
velocity profile, which is the velocity profile in the ![]() direction; and a pressure distribution
direction; and a pressure distribution ![]() . There are various ways to visualize the solution.
. There are various ways to visualize the solution.
The "InterpolationOrder" method option given to NDSolve specifies that both velocities are interpolated with second order and that the pressure is interpolated with first order. The "InterpolationOrder" option specification is equivalent to what is known in the finite element world as a Taylor–Hood element, and it helps stabilize the solution. Unfortunately, there is no known way to automatically set this option for specific PDEs, and it is recommended that the option be set for fluid flow PDEs that are based on the Navier–Stokes equation, like the FluidFlowPDEComponent.
Post-processing
Common visualization techniques
The computed pressure is a scalar field and as such can be visualized like any other scalar field. Contour or density plots are a good way to visualize these.
The velocity field is a vector-valued field. Here, vector, stream or line integral convolution plots are a good choice for visualization.
In two dimensions, a vorticity plot can also provide useful information.
Parametric Analysis
As a next step, it would be interesting to compare the flow field for various Reynolds numbers. ParametricNDSolve works just like NDSolve, with the addition that parameters can be specified. ParametricNDSolve then returns a function that, when fed numerical values for the parameters, computes the numerical solution. In this case, the Reynolds number is the parameter.
In the previous example, where NDSolve was used, the solution was stored in a list of the form {uVel,vVel,pressure}. Now, the solution of all simulation runs is stored in the variable solutions. Each entry in the solutions vector now contains an interpolation function for the ![]() field, the
field, the ![]() field and the pressure
field and the pressure ![]() .
.
Too large a Reynolds number will eventually prohibit convergence of the nonlinear PDE, as the PDE then becomes too strongly nonlinear. A failure in convergence is typically announced by a message from FindRoot, as FindRoot is the function that eventually solves the nonlinear equations within NDSolve. Not all hope is lost then, however. There are various measures that can be taken to extend the range in which a model converges.
There are various ways to circumvent the loss of convergence, which are discussed in the section Convergence of Fluid Flow Models. Here a closer look is taken at the mesh used for the analysis. In the above example, a mesh was generated automatically. One option is to make use of a mesh that is more appropriate for the problem at hand. The specifics of what "more appropriate" means depend on the problem at hand. For this example, note that the gradients of the ![]() - and
- and ![]() -velocity fields are largest at the top and at the right wall.
-velocity fields are largest at the top and at the right wall.
The generated mesh should reflect the steep gradients by having a finer resolution at steep gradients. Since the flow gradient is higher at the walls, a possible way to improve on that is to make use of a graded mesh. This can be done with the function ToGradedMesh. This allows for more refinement at the boundary, while not increasing the overall number of elements too much. Other refinement options like using a MeshRefinementFunction are also possible. More information about the mesh generation process can be found in the ElementMesh generation tutorial.
With the graded mesh, the overall number of elements is reduced and at the same time the element density increased near the walls.
See this note about improving the visual quality of the animation.
Since the driven cavity is a common fluid dynamics benchmark problem [6], literature data exists that can be used to compare numerical simulations.
The solution matches the literature values.
For computing even higher Reynolds numbers of the driven cavity example, see the section Convergence of Fluid Flow Models.
Time-Dependent Analysis
As a next workflow example, the time-dependent driven cavity example is solved. Now the fluid is initially at rest and the driving mechanism will ramp up with time. Everything else remains the same.
For the inflow boundary condition to be consistent with initial conditions, a helper function that smoothly ramps up the inflow over time is created.
It is possible to monitor the time integration.
See this note about improving the visual quality of the animation.
Equations
When planning a fluid flow simulation, a first step is to classify what flow regime is to be expected. For this, characteristic numbers that capture various aspects of flow behavior are used. One characterization is done through the Reynolds number ![]() . The Reynolds number is the ratio of internal force in the fluid to the fluid's viscosity.
. The Reynolds number is the ratio of internal force in the fluid to the fluid's viscosity.
Here ![]() [
[![]() ]is the dynamic viscosity,
]is the dynamic viscosity, ![]() [
[![]() ] is the density,
] is the density, ![]() [
[![]() ] is a typical flow velocity and
] is a typical flow velocity and ![]() [
[![]() ] is a characteristic length. The Reynolds number gives an approximate indication of what type of flow can be expected.
] is a characteristic length. The Reynolds number gives an approximate indication of what type of flow can be expected.
Flows with ![]() are in the creeping flow regime. For flows where the Reynolds number is larger than, say,
are in the creeping flow regime. For flows where the Reynolds number is larger than, say, ![]() , turbulence can appear. At what particular Reynolds number a flow transitions from laminar to turbulent depends on the specifics of that particular flow. For example, in tubes, a value of
, turbulence can appear. At what particular Reynolds number a flow transitions from laminar to turbulent depends on the specifics of that particular flow. For example, in tubes, a value of ![]() can induce turbulence flow. Contrary to that, flow along a flat plate will become turbulent only for
can induce turbulence flow. Contrary to that, flow along a flat plate will become turbulent only for ![]() .
.
A distinction is typically made between the following fluid flow regimes:
Honey, compared to water, is a viscous fluid. The higher the viscosity of a fluid, the more likely it will show laminar flow behavior. Gases, on the other hand have very low viscosity, and the Reynolds number approaches infinity. In most applications, gases are therefore considered to be inviscid, which means that for simplicity, their viscosity is assumed to be 0. Gases as also called inviscid fluids. In some applications, such an assumption is not possible, however.
Viscous laminar flow is described by a set of vector-valued equations called the Navier–Stokes equation. A wide range of fluid flow phenomena can be described with the Navier–Stokes equation, even beyond laminar flow. The Navier–Stokes equation is the overarching equation in fluid dynamics. The Navier–Stokes equation is a set of partial differential equations and exist in various forms, depending on the flow regime one is interested in.
Inviscid flow can be described by the Euler equations, which are not treated here.
The Navier–Stokes equation is a combination of a momentum equation and the continuity equation.
The momentum equation for a compressible fluid flow is a vector-valued equation expressed with the viscous stress tensor ![]() in [
in [![]() ]:
]:
The viscous stress tensor ![]() is given as:
is given as:
Inserting the definition of the viscous stress tensor ![]() into the momentum equation gives:
into the momentum equation gives:
Some formulations of the Navier–Stokes momentum equation contain an additional term ![]() called second viscosity, or volume viscosity, such that
called second viscosity, or volume viscosity, such that
but for most practical purposes, ![]() is negligible and
is negligible and ![]() .
.
The units of the momentum equations are a force density in [![]() ]. The conservation of momentum is essentially Newton's second law of motion for fluids. This can be seen when the equation is slightly rearranged:
]. The conservation of momentum is essentially Newton's second law of motion for fluids. This can be seen when the equation is slightly rearranged:
The momentum equation is almost always solved together with the mass continuity equation, which describes the conservation of mass:
with density ![]() the dependent variable and the fluid flow velocity vector
the dependent variable and the fluid flow velocity vector ![]() .
.
The Navier–Stokes equation is only valid when the smallest geometrical feature of the domain is still much larger then the mean free path of the fluid's molecules.
The Navier–Stokes equation is for compressible, weakly compressible and incompressible flow. Weakly compressible flow means that a pressure dependence of density can be neglected and is evaluated at a reference pressure.
For constant values of the mass density ![]() , the mass continuity equation simplifies to a volumetric continuity equation
, the mass continuity equation simplifies to a volumetric continuity equation ![]() , and with that, the viscous stress tensor simplifies to
, and with that, the viscous stress tensor simplifies to ![]() . When
. When ![]() is constant, it is possible to write
is constant, it is possible to write ![]() as
as ![]() , since in that case the divergence
, since in that case the divergence ![]() .
.
The incompressible form of the Navier–Stokes equation is:
The incompressible Navier–Stokes equation written out in component form is given as:
For a constant dynamics viscosity ![]() , this can be further simplified to:
, this can be further simplified to:
Newtonian versus non-Newtonian Flow
The viscosity of a non-Newtonian fluid changes with the applied forces. For a Newtonian fluid, such as water or honey, the viscosity does not change depending on how much the fluid is stirred. For non-Newtonian fluids, the amount of stirring changes the viscosity. Some materials become harder when they are stirred, while others become easier to stir. In practice, all gases and most liquids can be considered Newtonian. Non-Newtonian liquids are things like paint, blood, water-starch mixtures or liquid polymers.
In the following section, various non-Newtonian fluid flow models are introduced. For the derivation, consider the compressible Navier–Stokes equation:
Now it is possible to define the strain rate tensor ![]() in units of [1/s]:
in units of [1/s]:
Note that this strain rate looks very much like the infinitesimal strain measure defined in solid mechanics. In solid mechanics, the dependent variable ![]() is the displacement in [m] and
is the displacement in [m] and ![]() defines the infinitesimal strain. In fluid dynamics, the dependent variable
defines the infinitesimal strain. In fluid dynamics, the dependent variable ![]() is the velocity in [m/s] and
is the velocity in [m/s] and ![]() is a strain rate tensor. The strain rate tensor is also referred to as the rate or strain tensor.
is a strain rate tensor. The strain rate tensor is also referred to as the rate or strain tensor.
The viscous stress tensor ![]() in [Pa] for a Newtonian fluid is:
in [Pa] for a Newtonian fluid is:
This gives a different formulation for the Navier–Stokes equation:
For non-Newtonian fluids, the stress strain rate relation is nonlinear. This nonlinearity can be expressed in terms of an apparent viscosity ![]() , where the apparent viscosity is a function of the shear rate
, where the apparent viscosity is a function of the shear rate ![]() in [1/s]. Sometimes the apparent viscosity
in [1/s]. Sometimes the apparent viscosity ![]() is also called the effective viscosity.
is also called the effective viscosity.
For simplicity, but without restriction to generality, assume an incompressible non-Newtonian fluid, such that the ![]() term is not present. This assumption leads to:
term is not present. This assumption leads to:
The shear rate is computed as:
where ![]() is the contraction and computed by:
is the contraction and computed by:
A function to compute the shear rate is implanted as follows and is in the PDEModels` context:
ShearRate[strainRate_] :=
Sqrt[2 * TensorContract[strainRate * strainRate, {{1}, {2}}]];
The dynamic viscosity may depend on temperature and pressure, and for non-Newtonian fluids the dynamic viscosity additionally depends on the shear rate.
Different non-Newtonian constitutive models are used to express the apparent viscosity ![]() . The following non-Newtonian fluid flow models are implemented:
. The following non-Newtonian fluid flow models are implemented:
All models presented below the parameters pars need an entry for the "FluidDynamicsMaterialModel":
Power Law
The power law model is a commonly used non-Newtonian fluid model.
where ![]() is a factor that defaults to the dynamic viscosity
is a factor that defaults to the dynamic viscosity ![]() . The reference shear rate
. The reference shear rate ![]() has a default of 1 [1/s]. The default minimal shear rate
has a default of 1 [1/s]. The default minimal shear rate ![]() is set to
is set to ![]() [1/s]. The scalar
[1/s]. The scalar ![]() is an exponent. For
is an exponent. For ![]() , a Newtonian fluid is obtained, and as such, the power law implements a generalized Newtonian fluid model. For
, a Newtonian fluid is obtained, and as such, the power law implements a generalized Newtonian fluid model. For ![]() , the power law model results in a shear thinning fluid, also called a pseudo-plastic fluid. Paint, blood or ketchup falls in this category. For
, the power law model results in a shear thinning fluid, also called a pseudo-plastic fluid. Paint, blood or ketchup falls in this category. For ![]() , the result is a shear thickening fluid, also called dilatant fluids. An example for a shear thickening fluid is a mixture of water and cornstarch or quicksand.
, the result is a shear thickening fluid, also called dilatant fluids. An example for a shear thickening fluid is a mixture of water and cornstarch or quicksand.
The model given here deviates a bit from what is normally found in the literature. The original model predicts an infinite viscosity as the shear rate goes to zero. In real fluids, the shear rate tends to some constant value ![]() . This shortcoming of the original formulation is avoided by the formulation given here. A disadvantage of the power law model is that it cannot describe a Newtonian plateau. The Carreau model does that.
. This shortcoming of the original formulation is avoided by the formulation given here. A disadvantage of the power law model is that it cannot describe a Newtonian plateau. The Carreau model does that.
The power law is often given as an expression of the kinematic viscosity:
where ![]() is called the consistency index.
is called the consistency index.
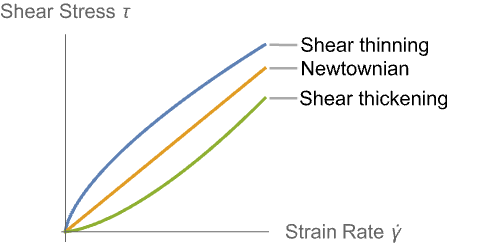
An illustration of shear flow versus Newtonian flow is given below.
Compare the strain rate versus shear stress for shear thickening and thinning flows with Newtonian flows.
It can be seen that for shear thinning fluids, the apparent viscosity is reduced for an increased strain rate, and for a shear thickening fluid, the apparent viscosity is increased for an increased strain rate.
The actual implementation of the power law model for non-Newtonian flow is given below, and the way this model is constructed can be used as an example for constructing other non-Newtonian flow models.
ApparentViscosity["PowerLaw", vars_, pars_, data__]:=
Module[
{model, strainRate, shearRate, m, apparentViscosity, minShearRate, n, refShearRate},
model = pars["FluidDynamicsMaterialModel"]["PowerLaw"];
minShearRate = model["MinimalShearRate"];
refShearRate = model["ReferenceShearRate"];
n = model["Exponent"];
m = model["PowerLawViscosity"];
strainRate = "StrainRate" /. data;
shearRate = PDEModels`ShearRate[strainRate];
apparentViscosity = m * (Max[shearRate, minShearRate]/refShearRate)^(n-1);
apparentViscosity
]
Power law example
The following section gives an example of a power law non-Newtonian flow.
In the given example, the kinematic viscosity is specified. Since the density is given as 1, the kinematic viscosity equals the dynamic viscosity ![]() .
.
To experiment, the power law exponent ![]() and the power law factor
and the power law factor ![]() are set as symbolic parameters.
are set as symbolic parameters.
The inflow profile is given as {1/2,0}, and at the outflow the pressure is set to 0. The walls are no-slip walls.
Carreau
The Carreau model also implements a generalized Newtonian flow model and is useful to model polymer or blood flows. The Carreau model implements:
where ![]() is the infinite shear rate viscosity,
is the infinite shear rate viscosity, ![]() is the zero shear rate viscosity,
is the zero shear rate viscosity, ![]() is a relaxation time with units [s],
is a relaxation time with units [s], ![]() is a power law exponent and
is a power law exponent and ![]() is a transition exponent, which controls the transition between Newtonian and power law models. For
is a transition exponent, which controls the transition between Newtonian and power law models. For ![]() or
or ![]() , this model reduces to the standard model of Newtonian fluid. For
, this model reduces to the standard model of Newtonian fluid. For ![]() , the Carreau model reduces to a Newtonian flow. For
, the Carreau model reduces to a Newtonian flow. For ![]() , the Carreau model approaches the power law model.
, the Carreau model approaches the power law model.
The model presented here is a generalization of the Carreau model usually called the Carreau–Yasuda model. The original Carreau model can be obtained through the default setting of ![]() .
.
The model enables the description of Newtonian plateaus for very small and very large shear rates. A Newtonian plateau is a phenomenon that is associated with some non-Newtonian fluids. Such fluids show constant viscosities for very small shear rates. This is called the primary plateau. The secondary plateau can be observed for very high shear rates.
The "TransitionExponent" parameter is optional. If not given a default value, ![]() is used.
is used.
The actual implementation of the Carreau model for non-Newtonian flow is given below, and the way this model is constructed can be used as an example for constructing other non-Newtonian flow models.
ApparentViscosity["Carreau", vars_, pars_, data__] :=
Module[
{model, mu0, muInf, n, a, lambda, strainRate, shearRate, apparentViscosity},
model = pars["FluidDynamicsMaterialModel"]["Carreau"];
mu0 = model["ZeroShearRateViscosity"];
muInf = model["InfiniteShearRateViscosity"];
n = model["PowerLawExponent"];
a = model["TransitionExponent"];
lambda = model["Lambda"];
strainRate = "StrainRate" /. data;
shearRate = ShearRate[strainRate + $MachineEpsilon];
apparentViscosity = muInf + (mu0 - muInf) *
(1 + (lambda * shearRate)^a )^((n - 1)/a);
apparentViscosity
]
A more detailed look at the parameters of the model could be useful. In what follows, several plots that show how the choice of parameters affects the apparent viscosity are presented. The model is considered with some fixed default parameters, the parameters are varied one by one, and the resulting apparent viscosities are compared. This will give a good idea how the choice of parameters affects the model. As the default choice of parameters, the following values are chosen:
The first parameter to vary is ![]() . This parameter is used to prescribe the viscosity of the fluid when the shear rate is equal to zero. The zero shear rate means that the fluid velocity is constant.
. This parameter is used to prescribe the viscosity of the fluid when the shear rate is equal to zero. The zero shear rate means that the fluid velocity is constant.
It can be seen from the plot that ![]() has an impact on the apparent viscosity
has an impact on the apparent viscosity ![]() for small values of the shear rate
for small values of the shear rate ![]() . Note that up until a shear rate of about 1/4, the plots exhibit a plateau, though not very pronounced. After that,
. Note that up until a shear rate of about 1/4, the plots exhibit a plateau, though not very pronounced. After that, ![]() drops. For higher values of the shear rate
drops. For higher values of the shear rate ![]() , the impact of
, the impact of ![]() on the apparent viscosity
on the apparent viscosity ![]() diminishes and becomes increasingly negligible, as can be seen in the plot below once the shear rate is expanded out further.
diminishes and becomes increasingly negligible, as can be seen in the plot below once the shear rate is expanded out further.
The secondary plateau is seen in the plot for the higher values of the shear rate ![]() . The zero shear rate viscosity
. The zero shear rate viscosity ![]() also influences how quickly the second plateau is approached.
also influences how quickly the second plateau is approached.
The parameter ![]() , on the other hand, describes how the viscosity behaves for higher values of the shear rate. It is the value to which the apparent viscosity converges if the shear rate goes to infinity.
, on the other hand, describes how the viscosity behaves for higher values of the shear rate. It is the value to which the apparent viscosity converges if the shear rate goes to infinity.
The effect of ![]() on the apparent viscosity
on the apparent viscosity ![]() increases as the shear rate
increases as the shear rate ![]() increases. A better insight can be obtained by considering larger values of the shear rate.
increases. A better insight can be obtained by considering larger values of the shear rate.
The value of ![]() plays a crucial role if the shear rate is large enough. It controls the value of the apparent viscosity at infinity.
plays a crucial role if the shear rate is large enough. It controls the value of the apparent viscosity at infinity.
The parameter ![]() represents the power law exponent. For values close to
represents the power law exponent. For values close to ![]() , the model resembles Newtonian fluid behavior. For values of
, the model resembles Newtonian fluid behavior. For values of ![]() smaller than 1, the apparent viscosity goes to
smaller than 1, the apparent viscosity goes to ![]() . For values of
. For values of ![]() larger than 1, the models mimics the power law model and the apparent viscosity goes to
larger than 1, the models mimics the power law model and the apparent viscosity goes to ![]() , where the sign depends on the sign of
, where the sign depends on the sign of ![]() .
.
It can be seen that the parameter ![]() controls how fast the apparent viscosity increases or decreases. The effect of
controls how fast the apparent viscosity increases or decreases. The effect of ![]() increases as the shear rate
increases as the shear rate ![]() increases.
increases.
The plot shows that the power law exponent ![]() affects how fast the apparent viscosity
affects how fast the apparent viscosity ![]() converges to
converges to ![]() . It should be noted that in the plots, all curves converge to
. It should be noted that in the plots, all curves converge to ![]() , even the curve associated with
, even the curve associated with ![]() . The convergence is just slow because the value of
. The convergence is just slow because the value of ![]() is close to 1.
is close to 1.
The parameter ![]() is the relaxation time. It controls how fast the model approaches
is the relaxation time. It controls how fast the model approaches ![]() .
.
The relaxation time ![]() plays an important role even for very small values of the shear rate, unlike the power law index
plays an important role even for very small values of the shear rate, unlike the power law index ![]() .
.
The relaxation time ![]() controls how fast the apparent viscosity approaches
controls how fast the apparent viscosity approaches ![]() . This is similar to the power law exponent
. This is similar to the power law exponent ![]() . The difference is that
. The difference is that ![]() is significant mostly for small values of the shear rate.
is significant mostly for small values of the shear rate.
The last parameter ![]() controls how fast the model transitions from the Newtonian to the non-Newtonian behavior. Increasing the values of
controls how fast the model transitions from the Newtonian to the non-Newtonian behavior. Increasing the values of ![]() will increase the threshold for the shear rate at which the model transitions from Newtonian to non-Newtonian behavior.
will increase the threshold for the shear rate at which the model transitions from Newtonian to non-Newtonian behavior.
It can be seen that the parameter ![]() controls the length of the primary plateau. But once the threshold is crossed and the fluid enters the non-Newtonian regime, then the apparent viscosities
controls the length of the primary plateau. But once the threshold is crossed and the fluid enters the non-Newtonian regime, then the apparent viscosities ![]() quickly converge to the same specific value.
quickly converge to the same specific value.
The impact of ![]() for higher values of the shear rate is negligible.
for higher values of the shear rate is negligible.
Cross
The cross model is an empirical model and is useful for polymer melts or polymeric solutions. The Carreau model can be used to model a cross power law:
where ![]() that can be specified by setting
that can be specified by setting ![]() .
.
Bingham–Papanastasiou
The Bingham–Papanastasiou model is useful for viscoplastic material. The Bingham–Papanastasiou model implements:
The actual implementation of the Bingham–Papanastasiou model for non-Newtonian flow is given below, and the way this model is constructed can be used as an example for constructing other non-Newtonian flow models.
ApparentViscosity["Bingham-Papanastasiou", vars_, pars_, data__]:=
Module[
{model, mup, sigma, m, strainRate, shearRate, apparentViscosity},
model = pars["FluidDynamicsMaterialModel"]["Bingham-Papanastasiou"];
mup = model["PlasticViscosity"];
sigma = model["YieldStress"];
m = model["ShearRateFactor"];
strainRate = "StrainRate" /. data;
shearRate = PDEModels`ShearRate[strainRate + $MachineEpsilon];
apparentViscosity = mup + sigma/shearRate * (1 - Exp[-m * shearRate]);
apparentViscosity
]
Herschel–Bulkley–Papanastasiou
The Herschel–Bulkley–Papanastasiou model implements:
The model uses a power law to compute the plastic viscosity of the Bingham–Papanastasiou model. All parameters for the power law and Bingham–Papanastasiou model can be specified, with the exception of the "PlasticViscosity", which is computed by the power law. The "MinimalShearRate" is set to ![]() .
.
ApparentViscosity["Herschel-Bulkley-Papanastasiou", vars_, pars_, data__]:=
Module[
{model, powerLawPars, mup, binghamPapanastasiouPars, apparentViscosity},
model = pars["FluidDynamicsMaterialModel"]["Herschel-Bulkley-Papanastasiou"];
powerLawPars = pars;
powerLawPars["FluidDynamicsMaterialModel"] = <|"PowerLaw" -> model|>;
mup = ApparentViscosity["PowerLaw", vars, powerLawPars, data];
binghamPapanastasiouPars = pars;
model["PlasticViscosity"] = mup;
binghamPapanastasiouPars["FluidDynamicsMaterialModel"] =
<|"Bingham-Papanastasiou"-> model|>;
apparentViscosity = ApparentViscosity["Bingham-Papanastasiou", vars,
binghamPapanastasiouPars, data];
apparentViscosity
]
Custom Apparent Viscosity Model
If your favorite model is not in the list given so far, it can, nevertheless, be used by specifying a custom viscosity model.
The function myApparentViscosity has the following signature:
myApparentViscosity[_, vars_, pars_, data__]:=
Module[{},
....
]
The function myApparentViscosity should return a scalar value for the apparent viscosity. Other models given in this monograph can serve as a template for writing an apparent viscosity function.
Custom Viscous Stress Tensor
The entire viscous stress tensor ![]() :
:
can be replaced by a function myViscousStressTensor.
The function myViscousStressTensor has the following signature:
myViscousStressTensor[vars_, pars_, data__]:=
Module[{},
....
]
The function myViscousStressTensor should return a viscous stress tensor.
Viscoelastic Flow
In viscoelastic flow, the viscous stress tensor ![]() in [Pa] for incompressible flow is given by:
in [Pa] for incompressible flow is given by:
where ![]() is a viscoelastic stress tensor. The equations involving viscoelastic flow can quickly become numerically unstable, and the usage of stabilization techniques is necessary. Since this version of NDSolve does not offer stabilization techniques, viscoelastic flow is not implemented currently.
is a viscoelastic stress tensor. The equations involving viscoelastic flow can quickly become numerically unstable, and the usage of stabilization techniques is necessary. Since this version of NDSolve does not offer stabilization techniques, viscoelastic flow is not implemented currently.
Energy Transport—Nonisothermal Flow
Often one wants to get an understanding of how temperature differences affect the flow of a fluid or how heat is transported with the fluid flow. To achieve this, the Navier–Stokes equation is coupled with a heat transfer equation:
where ![]() is absolute temperature in [
is absolute temperature in [![]() ],
], ![]() the specific heat capacity at a specific pressure in [
the specific heat capacity at a specific pressure in [![]() ],
], ![]() the thermal conductivity in [
the thermal conductivity in [![]() ] and
] and ![]() the heat source densities, or if you will, energy densities, in [
the heat source densities, or if you will, energy densities, in [![]() ]. A detailed explanation and derivation of the heat equation can be found in the Heat Transfer Monograph. Among the heat sources could be a viscous heating
]. A detailed explanation and derivation of the heat equation can be found in the Heat Transfer Monograph. Among the heat sources could be a viscous heating ![]() or terms that describe work done by changes in pressure. Both are often negligible but can be added if need be.
or terms that describe work done by changes in pressure. Both are often negligible but can be added if need be.
The key point is that a change in temperature induces a change in density. The volume increases and thus the weight decreases and the fluid rises: a temperature-dependent buoyancy force arises.
Boussinesq Approximation
A common simplification to model the coupling of the heat and Navier–Stokes equation is the Boussinesq approximation, which is based on the following assumptions [2, p.126]:
The first item allows the incompressible form of the continuity equation to be used:
The momentum equation is then given as:
Note the introduction of ![]() , and
, and ![]() is the gravitational field. The product of
is the gravitational field. The product of ![]() is the buoyancy contribution. As a further simplification, the Boussinesq approximation assumes a linear relation between the density
is the buoyancy contribution. As a further simplification, the Boussinesq approximation assumes a linear relation between the density ![]() and temperature
and temperature ![]() :
:
where ![]() is the thermal expansion coefficient and
is the thermal expansion coefficient and ![]() and
and ![]() are reference values. In fact, the equation is a first-order Taylor expansion around
are reference values. In fact, the equation is a first-order Taylor expansion around ![]() . It should be noted that the linear relationship between
. It should be noted that the linear relationship between ![]() and
and ![]() needs to be replaced with a close-to-quadratic relationship for special cases, like pure water at
needs to be replaced with a close-to-quadratic relationship for special cases, like pure water at ![]() [4].
[4].
The Boussinesq approximation provides a coupling between the flow equations and the heat transfer model. A temperature difference is now capable of driving the fluid flow: If a flow field is isothermal, that means ![]() , then the fluid will remain at rest. If, however, one wall is heated, a buoyancy force will drive the fluid flow.
, then the fluid will remain at rest. If, however, one wall is heated, a buoyancy force will drive the fluid flow.
Some caution needs to be exercised when making use of the Boussinesq approximation: The only material parameter that is varying is the density ![]() in the buoyancy term. That means all other occurrences of the density and also the dynamic viscosity
in the buoyancy term. That means all other occurrences of the density and also the dynamic viscosity ![]() , the thermal expansion coefficient
, the thermal expansion coefficient ![]() , the specific heat capacity
, the specific heat capacity ![]() and the thermal conductivity
and the thermal conductivity ![]() are constant in the interval
are constant in the interval ![]() . The Boussinesq approximation assumes that the pressure is constant. The density in the buoyancy term is a Taylor expansion where
. The Boussinesq approximation assumes that the pressure is constant. The density in the buoyancy term is a Taylor expansion where ![]() is the expansion point.
is the expansion point.
The restrictions pointed out above are quite severe, and it is advisable to make sure that the conditions are satisfied. Some effort was made to derive the following criteria [2; 5]:
Here, ![]() is the maximal temperature fluctuation around
is the maximal temperature fluctuation around ![]() and
and ![]() is a characteristic length.
is a characteristic length.
The following example illustrates this procedure for water [2, p. 133]. To make an estimate of when the approximation is valid, the inequalities from above are encoded.
The water at ![]() and
and ![]() has the following parameters [5]:
has the following parameters [5]:
The same can also be done considering the pressure [5]. One final remark is that for integrating quantities that involve the material constants, the reference values like ![]() should be used and not the temperature-dependent density
should be used and not the temperature-dependent density ![]() used in the buoyancy force term [4].
used in the buoyancy force term [4].
Rayleigh–Bénard Convection
A Rayleigh–Bénard convection is presented as an application of the Boussinesq approximation. In this example, a rectangular region is filled with a fluid. The side walls are insulated and the top and bottom walls are cooled and heated, respectively. First, a region and some parameters are specified.
The rectangle has an aspect ratio of 4:1.
Set up a viscous Navier–Stokes equation that is coupled to a heat equation making use of a Boussinesq approximation. Use the material parameters specified.
Boundary conditions and initial conditions need to be set up.
Monitor the time integration progress and the total time it takes to solve the PDE while using a refined mesh and interpolating the velocities ![]() and
and ![]() and the temperature
and the temperature ![]() with second order and the pressure
with second order and the pressure ![]() with first order.
with first order.
The last step is post-processing.
Further examples for heat transfer with fluid flow can be found in the model collection example Buoyancy-Driven Flow, where a Reynolds number–based model is used, and a second example, Heat Exchange, uses a standard model. The example Thermal Decomposition shows a coupling of heat, mass and fluid transport.
Flow Boundary Conditions
The geometrical domain of a fluid flow model is finite. At the boundaries of the domain, boundary conditions are needed to model the surroundings in which the flow is embedded. Boundary conditions describe domain walls or inflows into or outflows out of a domain. To make it easier to talk about boundary conditions, it is useful to introduce some terminology. Let ![]() denote a velocity component normal to a boundary and
denote a velocity component normal to a boundary and ![]() denote a velocity component tangential to a boundary.
denote a velocity component tangential to a boundary. ![]() and
and ![]() denote the derivatives of both components in the normal direction.
denote the derivatives of both components in the normal direction.
Consider for simplicity a 2D geometry that is parallel to the ![]() and
and ![]() axes, like the lid-driven cavity example from the introduction. There are two cases: upright boundaries and horizontal boundaries. For the upright boundary, there is:
axes, like the lid-driven cavity example from the introduction. There are two cases: upright boundaries and horizontal boundaries. For the upright boundary, there is:
At a upright boundary, marked in light red, a normal fluid flow component is ![]() and tangential fluid flow component is
and tangential fluid flow component is ![]() .
.
For horizontal boundaries, there is:
At a horizontal boundary, marked in light red, a normal fluid flow component is ![]() and tangential fluid flow component is
and tangential fluid flow component is ![]() .
.
In cases where the boundary is not axis-aligned, the components ![]() and
and ![]() need to be computed from
need to be computed from ![]() and
and ![]() .
.
Inflow Conditions
An inflow is also called an inlet. Both velocity components are prescribed:
Here ![]() and
and ![]() are the normal and tangential components of the velocity vector
are the normal and tangential components of the velocity vector ![]() . To specify the inflow condition,
. To specify the inflow condition, ![]() and
and ![]() are given. A typical inflow profile is:
are given. A typical inflow profile is:
where ![]() is a function that specifies a fluid velocity in the normal direction.
is a function that specifies a fluid velocity in the normal direction.
One thing to keep in mind is that the inflow condition needs to be consistent with adjacent boundary conditions. For example, if the inflow profile at the boundary of the inlet is 0, then a non-slip wall boundary can be used. If the inflow profile is nonzero at the boundary of the inlet, then using an adjacent no-slip wall boundary condition will make it hard, if not impossible, for the solver to converge the model. In some cases, when the inflow condition at the boundary is nonzero, it may make sense to use a slip wall boundary condition instead.
An easy way to create a parabolic inflow profile is by using Fit. Say, there is an inflow from ![]() and a maximum inflow velocity of 1 [
and a maximum inflow velocity of 1 [![]() ] is given.
] is given.
Outflow Conditions
An outflow is also called an outlet. Both velocity components remain constant with respect to the normal:
Wall Conditions
A wall is any impermeable boundary containing a fluid. One condition at the wall boundary is then that the fluid cannot flow through the wall. A minimal requirement is that:
If only this minimal requirement is satisfied, the condition is called a slip condition. A second requirement is often that additionally there should be no fluid flow tangential to the wall boundary. In this second case, the condition is called a no-slip condition.
Pay attention that wall boundary conditions are consistent with inflow boundary conditions. For more details, see the section on Inflow Conditions.
No-slip
A typical wall boundary condition is the no-slip condition. No-slip means that first, there is no fluid going through the wall and second, that the fluid adheres to the wall. The second condition models friction at the boundary. In sum, this means that:
Thus, the fluid flow velocity vector is set to 0 at this boundary:
This can be set with a DirichletCondition.
No-slip example
This example shows the application of a no-slip wall boundary condition. A rectangular flow region with two semi-disk cutouts is considered. On the left there is an inflow profile and on the right there is an outflow condition. The remainder of the domain are walls modeled as a no-slip boundary condition.
Note that at ![]() and at
and at ![]() the velocity is 0.
the velocity is 0.
Note that at ![]() and at
and at ![]() the velocity is 0.
the velocity is 0.
Slip
In the slip, there is still no fluid going through the wall, but contrary to the no-slip condition, in the slip case there are no losses due to friction; this means that:
In the axis-aligned case, the following holds for a upright wall:
In the axis-aligned case, the following holds for a horizontal wall:
Traction
Consider the Navier–Stokes momentum equation:
The viscous stress tensor ![]() is given as:
is given as:
where ![]() is the total stress. The total stress is the viscous stress
is the total stress. The total stress is the viscous stress ![]() plus the pressure component.
plus the pressure component.
To prescribe traction, it is necessary to specify
where ![]() is a traction value vector. With all terms substituted:
is a traction value vector. With all terms substituted:
The total stress tensor ![]() in component form is:
in component form is:
The type of boundary conditions can be specified through NeumannValue.
Traction example
The following example considers a flow with prescribed traction boundary conditions in an annulus region. On the outer edge, at ![]() , there are the no-slip boundary conditions. These set the fluid velocity in the
, there are the no-slip boundary conditions. These set the fluid velocity in the ![]() and
and ![]() directions to 0,
directions to 0, ![]() .
.
On the inner boundary, at ![]() , instead of defining a velocity, a traction is prescribed. The traction with the stress vector
, instead of defining a velocity, a traction is prescribed. The traction with the stress vector ![]() is given as:
is given as:
Here, ![]() is the radial unit vector given as
is the radial unit vector given as ![]() and
and ![]() is the tangent unit vector given as
is the tangent unit vector given as ![]() .
. ![]() and
and ![]() are the Cartesian unit vectors in the
are the Cartesian unit vectors in the ![]() axis and
axis and ![]() axis directions, respectively. For this example, the traction in the normal direction is set to
axis directions, respectively. For this example, the traction in the normal direction is set to ![]() and the tangential traction to
and the tangential traction to ![]() . This means that there is no flow across the inner boundary but only tangentially to it.
. This means that there is no flow across the inner boundary but only tangentially to it.
On the outer boundary there is the no-slip condition.
On the inner surface, the tangent unit normal can be computed from the outward-pointing unit normal ![]() with a cross product.
with a cross product.
To extract the first and second components of the cross product for the ![]() and
and ![]() directions, respectively, Indexed is used.
directions, respectively, Indexed is used.
Equivalently, the tangent unit normal can also be given as ![]() , because the unit normal vector on the inner surface is
, because the unit normal vector on the inner surface is ![]() and the unit tangent then is
and the unit tangent then is ![]() .
.
Without specifying a boundary condition for the pressure, the pressure value will be floating and NDSolve will give a warning that not enough boundary conditions are specified.
To verify that the traction boundary condition works, the radial and tangential components of the velocities can be computed and plotted at ![]() for all
for all ![]() . For the radial velocity, a solution proportional to
. For the radial velocity, a solution proportional to ![]() is expected, and for the tangential velocity, a solution proportional to
is expected, and for the tangential velocity, a solution proportional to ![]() is expected.
is expected.
The next step is to compute the normal stress and the shear at the inner boundary and check that they match the prescribed traction boundary conditions. The total stress tensor is given by:
The normal and tangential components of the traction vector can be computed by:
Initial Conditions
For time-dependent problems initial conditions ![]() need to be specified.
need to be specified.
Initial conditions ![]() need to satisfy the continuity equation.
need to satisfy the continuity equation.
Convergence of Fluid Flow Models
Fluid flow PDEs can be difficult to get to converge. This section provides hints at what to try when NDSolve cannot find a solution to a fluid flow model. Combinations of the methods presented here are possible.
Initial Seeding
Typically, nonlinear solvers need an initial guess, a seed to get started. If this seed is too far off from the solution, the solver cannot converge. The radius in which the solver converges is called the radius of convergence. The closer the initial seed is to the final solution, the better.
Iterative stepping
Here the solution of a low Reynolds number flow field is used to seed the computation of a higher Reynolds number. For this, the parametric function is used.
Specifying the dependent variables helps the solver to create an optimized system of equations.
Equation Modification
This may sound absurd at first; why would you modify the equation? Sometimes it is possible that a more stable or reduced set of equations can be used. The solution can then be used as a seed for the full equations.
Stokes equation
When no initial seed is specified, the solver assumes 0 for all dependent variables. In the case of fluid dynamics, when an initial seed of 0 is used for the velocity field and pressure is used, you are in effect solving a Stokes-type equation.
References
1. Simple Fields of Physics; Backstrom, G.; 2006; GB Publishing; ISBN 91-975553-0-4
2. Numerische Simulation in der Strömungsmechanik; Griebel M. et al.; 1995; Vieweg; ISBN 3-528-06761-6
3. The Efficient Engineer; https://www.youtube.com/watch?v=VvDJyhYSJv8; retrieved 2022/12/05
4. "On the Use and Misuse of the Oberbeck–Boussinesq Approximation"; Barletta, A.; Celli, M; Rees, D.A.S; https://arxiv.org/abs/2202.10981
5. "The Validity of the Boussinesq Approximation for Liquids and Gases"; Gray, D.; Giorini, A.; International Journal of Heat and Mass Transfer, Volume 19, Issue 5, May 1976, pp. 545–551; https://doi.org/10.1016/0017-9310(76)90168-X
6. “High-Re Solutions for Incompressible Flow Using the Navier-Stokes Equations and a Multigrid Method"; Ghia, U., Ghia, K.N., Shin, C.T.; Journal of Computational Physics, vol. 48, pp. 387–411, 1982.; https://doi.org/10.1016/0021-9991(82)90058-4