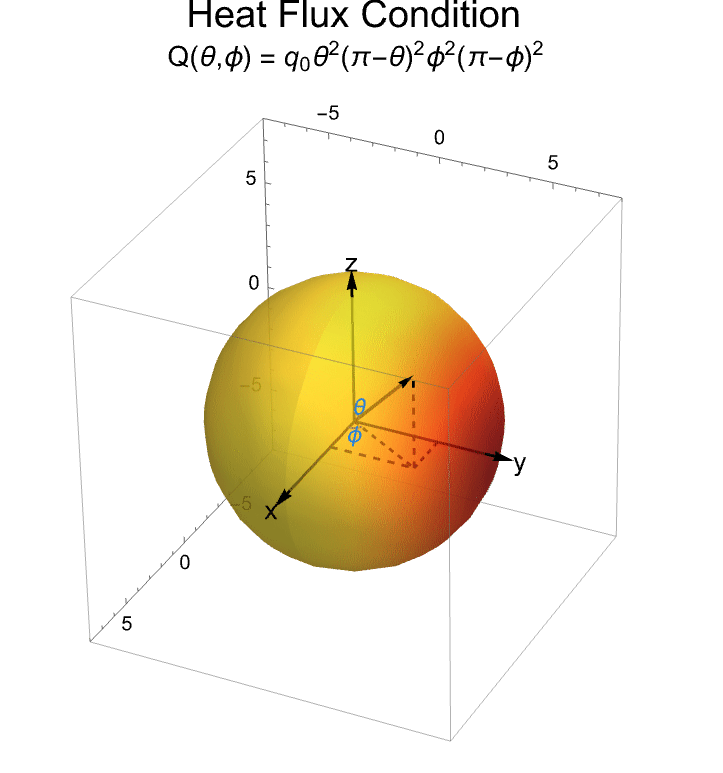Heat Conduction in a Multilayer Sphere
| Introduction | Solve the PDE Heat Transfer Model |
| Domain and Mesh Generation | Post-processing and Visualization |
| Heat Transfer Model | Nomenclature |
| Initial and Boundary Conditions | References |
Introduction
Devices constructed by layers of multiple materials have been used in many industrial applications, such as chemical, mechanical and aerospace engineering. One important feature of multilayered materials lies in the possibility to combine several thermal properties. Performing numerical simulations and obtaining the temperature distribution of such compounds are important because they give insights into how the real system will behave.
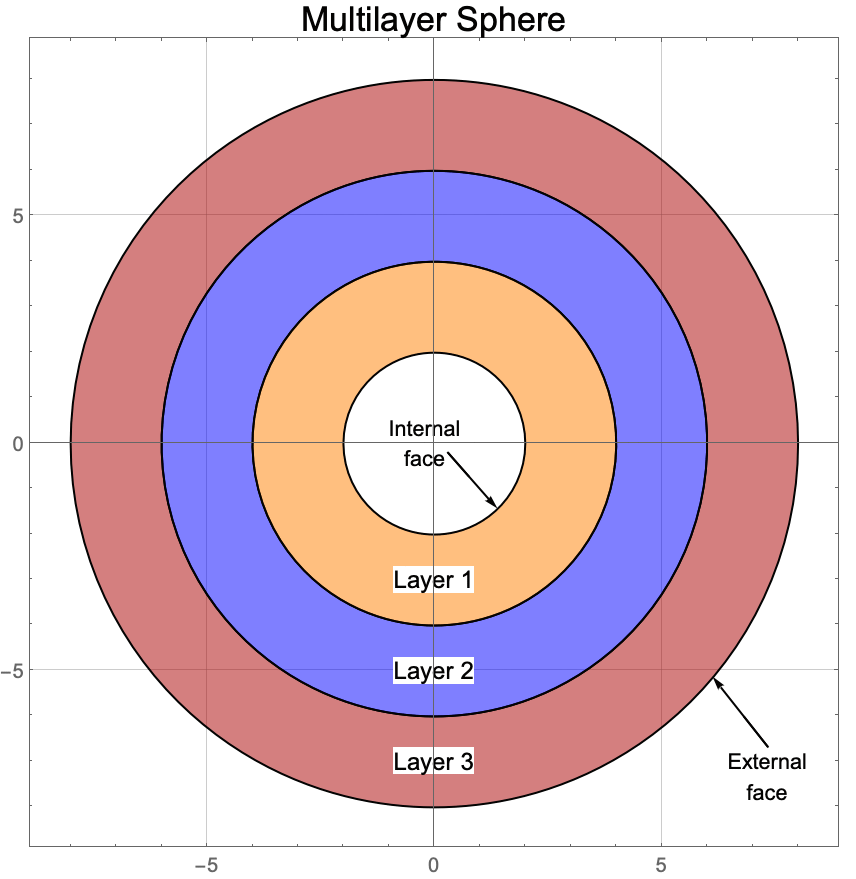
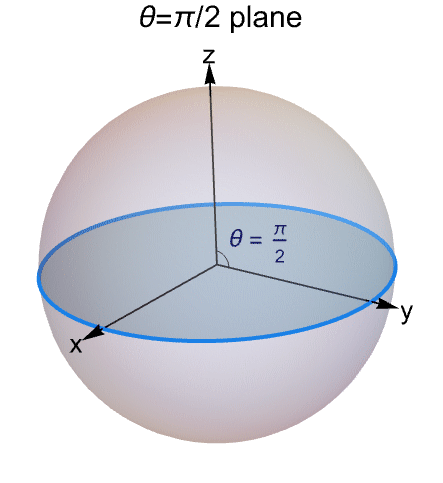
This model is based on [Singh et al., 2016] in which a 3D heat transfer transport through a multilayered sphere was analyzed. The problem statement is to perform a thermal analysis and find the temperature field distribution ![]() at time
at time ![]() of
of ![]() concentric hollow spherical layers in thermal contact. A 2D cross section of the geometry is shown for
concentric hollow spherical layers in thermal contact. A 2D cross section of the geometry is shown for ![]() .
.
Each layer of the sphere has specific material properties; for example, the ![]() th layer will have a thermal conductivity
th layer will have a thermal conductivity ![]() , mass density
, mass density ![]() and specific heat capacity
and specific heat capacity ![]() . This simulation is limited to three layers—three concentric hollow spheres—and
. This simulation is limited to three layers—three concentric hollow spheres—and ![]() . As mentioned in [Singh et al., 2016], two different types of boundary conditions are imposed, one at the external face and a second type at the internal face of the multilayer sphere setup. In this model, the external face of the hollow sphere is subjected to a nonlinear heat source
. As mentioned in [Singh et al., 2016], two different types of boundary conditions are imposed, one at the external face and a second type at the internal face of the multilayer sphere setup. In this model, the external face of the hollow sphere is subjected to a nonlinear heat source ![]() at all times, and the internal face of the first layer will be set to a fixed temperature of
at all times, and the internal face of the first layer will be set to a fixed temperature of ![]() . The simulation starts with an initial temperature of
. The simulation starts with an initial temperature of ![]() for all layers of the sphere. As heat transfers between layers, the temperature change of each layer will depend, as expected, on its thermal properties.
for all layers of the sphere. As heat transfers between layers, the temperature change of each layer will depend, as expected, on its thermal properties.
Refer to the information provided in Heat Transfer for a more general theoretical background on heat transfer analysis.
Domain and Mesh Generation
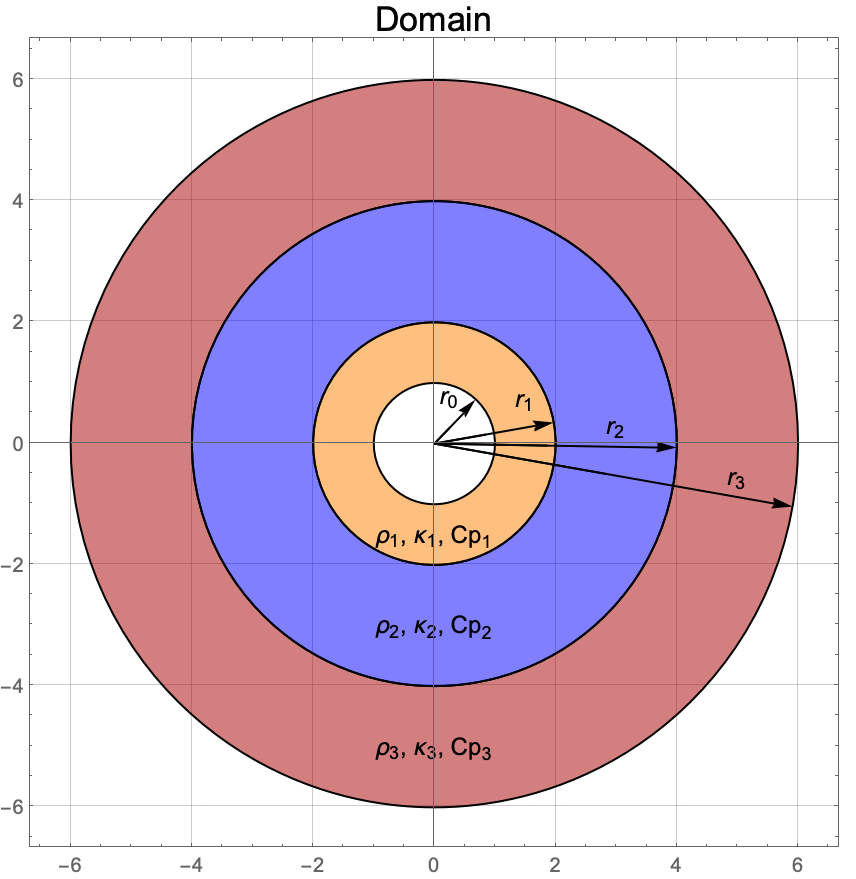
The following plot shows a two-dimensional cross sectional cut through the three concentric spherical layers. Indicated are the radii ri and the model parameter labels of each layer ![]() ,
, ![]() and
and ![]() .
.
Next, the faces are combined. This will result in an object with four regions, ![]() ,
, ![]() . The multilayered sphere is hollow in the region
. The multilayered sphere is hollow in the region ![]() . This requirement can be specified during the mesh generation with the ToElementMesh option RegionHoles.
. This requirement can be specified during the mesh generation with the ToElementMesh option RegionHoles.
The three layers will be labeled with three markers 1, 2 and 3. For more information on markers and their generation in meshes, see the "Element Mesh Generation" tutorial.
Heat Transfer Model
A transient heat transfer equation (1) will be used to determine the temperature field distribution ![]() :
:
For this PDE model, two boundary conditions will be applied to the inner face (![]() ) and the external face (
) and the external face (![]() ) of the multilayer sphere. On the inner face, a surface boundary condition of constant temperature equal to
) of the multilayer sphere. On the inner face, a surface boundary condition of constant temperature equal to ![]() will be imposed. On the external face, a nonlinear heat flux source of value
will be imposed. On the external face, a nonlinear heat flux source of value ![]() will be imposed, where
will be imposed, where ![]() is the polar angle and
is the polar angle and ![]() is the azimuthal angle in spherical coordinates.
is the azimuthal angle in spherical coordinates.
Also, see this note about how to set up of computationally efficient PDE coefficients.
Initial and Boundary Conditions
For this PDE model, the internal face of layer 1 will be set to a temperature surface boundary condition of c. The external face of layer 3 will be subjected to a nonuniform time-independent heat flux condition ![]() that depends on the polar angle
that depends on the polar angle ![]() and the azimuthal angle
and the azimuthal angle ![]() . The problem description in [Singh et al., 2016] is formulated in spherical coordinates. To apply the boundary conditions, originally defined in spherical coordinates, a coordinate transformation from spherical coordinates to Cartesian coordinates is performed.
. The problem description in [Singh et al., 2016] is formulated in spherical coordinates. To apply the boundary conditions, originally defined in spherical coordinates, a coordinate transformation from spherical coordinates to Cartesian coordinates is performed.
First, a DirichletCondition is set up with the help of the HeatTemperatureCondition function.
The NeumannValue on the outside of the sphere is created with the help of the HeatFluxValue function. The heat-flux source is applied on the external face of layer 3.
The following plot shows the heat flux boundary condition and the coordinate system used to formulate the problem. The heat flux has its peak value ![]() at
at ![]() , and it decreases to 0 in the region
, and it decreases to 0 in the region ![]() :
:
Solve the PDE Heat Transfer Model
To analyze the heat conduction between the three layers, the model is solved from ![]() to
to ![]() .
.
Post-processing and Visualization
Next, 1D, 2D and 3D cuts of the temperature field distribution ![]() of the multilayered sphere are visualized.
of the multilayered sphere are visualized.
1-Dimensional Cut: Temperature Distribution in Radial Direction
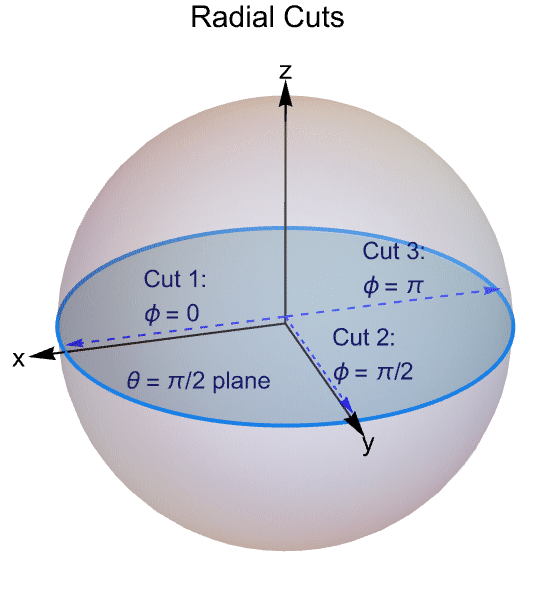
The transient temperature distribution solutions are plotted in the radial direction along ![]() and the azimuthal (
and the azimuthal (![]() ) directions: a)
) directions: a) ![]() , b)
, b) ![]() and c)
and c) ![]() .
.
The linear section ![]() corresponds to
corresponds to ![]() ,
, ![]() corresponds to
corresponds to ![]() , and
, and ![]() corresponds to
corresponds to ![]() .
.
2-Dimensional Cut: Temperature Contour Plot Distribution
Visualize the temperature field contours in the ![]() cross section of the sphere. The temperature distribution of the whole system increases with time. For each time in
cross section of the sphere. The temperature distribution of the whole system increases with time. For each time in ![]() , a list of nine temperature values is defined to plot as contours.
, a list of nine temperature values is defined to plot as contours.
3-Dimensional Cut: Temperature Density Plot Animation
A time animation is performed of the temperature field distribution in a 3D section of the sphere. When the heat source is applied from the region ![]() , the temperature starts to increase in the
, the temperature starts to increase in the ![]() direction, as can be seen in the animation below. Since the relationship between thermal conductivities of each layer is
direction, as can be seen in the animation below. Since the relationship between thermal conductivities of each layer is ![]() , layer 3 (outer layer) transports heat and increases its temperature faster than the internal layer, as can be seen in the density plot animation.
, layer 3 (outer layer) transports heat and increases its temperature faster than the internal layer, as can be seen in the density plot animation.
A limit in the plot range of the SliceContourPlot3D is used, and the reason is that if the center sphere of the slice surface "CenterCutSphere" is exactly the same sphere as the region of the mesh it is plotted over, part of the surface will not be displayed. Therefore, the range of the plot must be smaller than the region of the mesh.
The 3D animations that follow can require an above-average amount of disk space. To reduce the disk space this notebook requires, the function Rasterize is called on the visualization. The disadvantage of this is that the quality of the animation will not be as sharp as without it. To obtain high-quality graphics, remove the call to Rasterize.
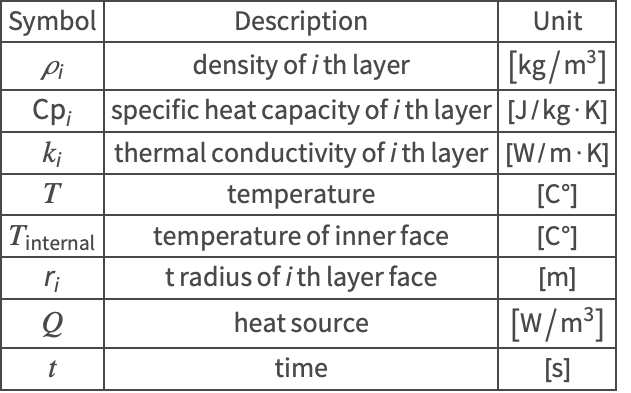
Nomenclature
References
1. Suneet, S., Jain, P. K. and Uddin, R. "Analytical Solution for Three-Dimensional, Unsteady Heat Conduction in a Multilayer Sphere." ASME Journal of Heat Transfer, 2016, 138(10), 101301. doi: 10.1115/1.4033536.