SliceContourPlot3D[f,surf,{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}]
generates a contour plot of f over the slice surface surf as a function of x, y, and z.
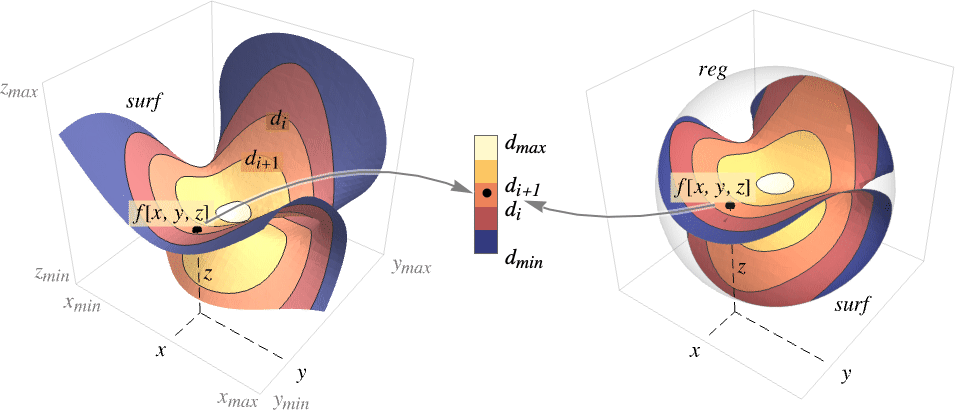
SliceContourPlot3D[f,surf,{x,y,z}∈reg]
restricts the surface to be within region reg.
SliceContourPlot3D[f,{surf1,surf2,…},…]
generates contour plots over several slices.




SliceContourPlot3D
SliceContourPlot3D[f,surf,{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}]
generates a contour plot of f over the slice surface surf as a function of x, y, and z.
SliceContourPlot3D[f,surf,{x,y,z}∈reg]
restricts the surface to be within region reg.
SliceContourPlot3D[f,{surf1,surf2,…},…]
generates contour plots over several slices.
Details and Options






- SliceContourPlot3D constructs contour curves on the surface surf corresponding to the level sets where f[x,y,z] has constant values d1, d2, etc. By default, the regions between the curves are shaded to more easily identify regions whose values are between di and di+1.
- It visualizes the areas
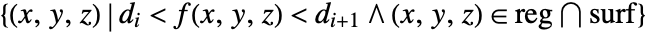 .
. - The following basic slice surfaces surfi can be given:
-
Automatic automatically determine slice surfaces 
"CenterPlanes" coordinate planes through the center 
"BackPlanes" coordinate planes at the back of the plot 
"XStackedPlanes" coordinate planes stacked along 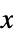 axis
axis
"YStackedPlanes" coordinate planes stacked along 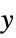 axis
axis
"ZStackedPlanes" coordinate planes stacked along 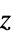 axis
axis
"DiagonalStackedPlanes" planes stacked diagonally 
"CenterSphere" a sphere in the center 
"CenterCutSphere" a sphere with a cutout wedge 
"CenterCutBox" a box with a cutout octant - SliceContourPlot3D[f,{x,xmin,xmax},…] is equivalent to SliceContourPlot3D[f,Automatic,{x,xmin,xmax},…] etc.
- The following parametrizations can be used for basic slice surfaces:
-
{"XStackedPlanes",n}, generate n equally spaced planes {"XStackedPlanes",{x1,x2,…}} generate planes for 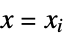
{"CenterCutSphere",ϕopen} cut angle ϕopen facing the view point {"CenterCutSphere",ϕopen,ϕcenter} cut angle ϕopen with center angle ϕcenter in the 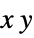 plane
plane - "YStackedPlanes", "ZStackedPlanes" follow the specifications for "XStackedPlanes", with additional features shown in the scope examples.
- The following general slice surfaces surfi can be used:
-
expr0 implicit equation in x, y, and z, e.g. x y z-10 surfaceregion a two-dimensional region in 3D, e.g. Hyperplane volumeregion a three-dimensional region in 3D where surfi is taken as the boundary surface, e.g. Cuboid - The following wrappers can be used for slice surfaces surfi:
-
Annotation[surf,label] provide an annotation Button[surf,action] define an action to execute when the surface is clicked EventHandler[surf,…] define a general event handler for the surface Hyperlink[surf,uri] make the surface act as a hyperlink PopupWindow[surf,cont] attach a popup window to the surface StatusArea[surf,label] display in status area when the surface is moused over Tooltip[surf,label] attach an arbitrary tooltip to the surface - SliceContourPlot3D has the same options as Graphics3D, with the following additions and changes: [List of all options]
-
Axes True whether to draw axes BoundaryStyle Automatic how to style surface boundaries BoxRatios {1,1,1} bounding 3D box ratios ClippingStyle None how to draw values clipped by PlotRange ColorFunction Automatic how to color the plot ColorFunctionScaling True whether to scale the arguments to ColorFunction Contours Automatic how many or what contours to show ContourShading Automatic how to shade regions between contours ContourStyle Automatic the style for contour lines PerformanceGoal $PerformanceGoal aspects of performance to optimize PlotLegends None legends for color gradients PlotPoints Automatic initial number of samples for the function f and slice surfaces surfi in each direction PlotRange {Full,Full,Full,Automatic} range of f or other values to include PlotTheme $PlotTheme overall theme for the plot RegionFunction (True&) how to determine whether a point should be included ScalingFunctions None how to scale individual coordinates TargetUnits Automatic desired units to use WorkingPrecision MachinePrecision the precision used in internal computations - ColorFunction is by default supplied with the scaled value of f.
- RegionFunction is by default supplied with x, y, z and f.
- Possible settings for ScalingFunctions include:
-
sf scale the f contour values {sx,sy,sz} scale x, y and z axes {sx,sy,sz,sf} scale x, y and z axes and f contour values - Common built-in scaling functions s include:
-
"Log" 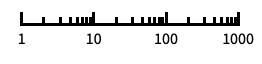
log scale with automatic tick labeling "Log10" 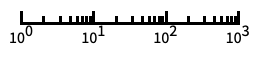
base-10 log scale with powers of 10 for ticks "SignedLog" 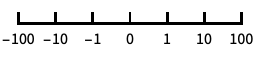
log-like scale that includes 0 and negative numbers "Reverse" 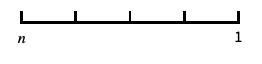
reverse the coordinate direction "Infinite" 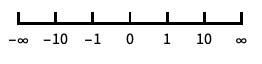
infinite scale -
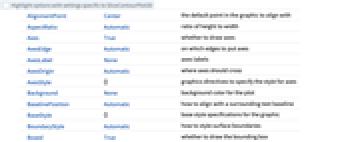
AlignmentPoint Center the default point in the graphic to align with AspectRatio Automatic ratio of height to width Axes True whether to draw axes AxesEdge Automatic on which edges to put axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} graphics directives to specify the style for axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic BoundaryStyle Automatic how to style surface boundaries Boxed True whether to draw the bounding box BoxRatios {1,1,1} bounding 3D box ratios BoxStyle {} style specifications for the box ClippingStyle None how to draw values clipped by PlotRange ClipPlanes None clipping planes ClipPlanesStyle Automatic style specifications for clipping planes ColorFunction Automatic how to color the plot ColorFunctionScaling True whether to scale the arguments to ColorFunction ContentSelectable Automatic whether to allow contents to be selected Contours Automatic how many or what contours to show ContourShading Automatic how to shade regions between contours ContourStyle Automatic the style for contour lines ControllerLinking False when to link to external rotation controllers ControllerPath Automatic what external controllers to try to use Epilog {} 2D graphics primitives to be rendered after the main plot FaceGrids None grid lines to draw on the bounding box FaceGridsStyle {} style specifications for face grids FormatType TraditionalForm default format type for text ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels, etc. ImageSize Automatic absolute size at which to render the graphic LabelStyle {} style specifications for labels Lighting Automatic simulated light sources to use Method Automatic details of 3D graphics methods to use PerformanceGoal $PerformanceGoal aspects of performance to optimize PlotLabel None a label for the plot PlotLegends None legends for color gradients PlotPoints Automatic initial number of samples for the function f and slice surfaces surfi in each direction PlotRange {Full,Full,Full,Automatic} range of f or other values to include PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic final display region to be filled PlotTheme $PlotTheme overall theme for the plot PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} 2D graphics primitives to be rendered before the main plot RegionFunction (True&) how to determine whether a point should be included RotationAction "Fit" how to render after interactive rotation ScalingFunctions None how to scale individual coordinates SphericalRegion Automatic whether to make the circumscribing sphere fit in the final display area TargetUnits Automatic desired units to use Ticks Automatic specification for ticks TicksStyle {} style specification for ticks TouchscreenAutoZoom False whether to zoom to fullscreen when activated on a touchscreen ViewAngle Automatic angle of the field of view ViewCenter Automatic point to display at the center ViewMatrix Automatic explicit transformation matrix ViewPoint {1.3,-2.4,2.} viewing position ViewProjection Automatic projection method for rendering objects distant from the viewer ViewRange All range of viewing distances to include ViewVector Automatic position and direction of a simulated camera ViewVertical {0,0,1} direction to make vertical WorkingPrecision MachinePrecision the precision used in internal computations
List of all options




Examples
open all close allBasic Examples (2)
Scope (24)
Surfaces (9)
Generate a contour plot over standard slice surfaces:
Standard axis-aligned stacked slice surfaces:
Plot the contours over any surface region:
Plotting over a volume primitive is equivalent to plotting over RegionBoundary[reg]:
Plot the contours over the surface ![]() :
:
Plot the contours over multiple surfaces:
Sampling (4)
Use Contours to specify the number of contours:
Or the list of function values ![]() to put contours:
to put contours:
Areas where the function becomes nonreal are excluded:
Use RegionFunction to expose obscured slices:
The domain may be specified by a region including Cone:
A formula region including ImplicitRegion:
A mesh-based region including BoundaryMeshRegion:
Presentation (11)
Use PlotTheme to immediately get overall styling:
Use PlotLegends to get a color bar for the different values:
Control the display of axes with Axes:
Label axes using AxesLabel and the whole plot using PlotLabel:
Color the plot by the function values with ColorFunction:
Style regions between contours with ContourShading:
Use ContourStyle to style the contour lines:
Style the slice surface boundaries with BoundaryStyle:
TargetUnits specifies which units to use in the visualization:
Options (71)
Axes (3)
AxesLabel (4)
No axes labels are drawn by default:
Use specific labels for each axis:
Use labels based on variables specified in SliceContourPlot3D:
AxesOrigin (2)
AxesStyle (3)
BoundaryStyle (1)
Style the slice surface boundaries with BoundaryStyle:
BoxRatios (3)
ClippingStyle (2)
ColorFunction (3)
ColorFunctionScaling (2)
Contours (4)
ContourShading (4)
ContourShadingAutomatic computes contour region shading from the ColorFunction:
Cyclically repeat shading styles:
Leave every third contour region empty, starting from the second:
ImageSize (7)
Use named sizes such as Tiny, Small, Medium and Large:
Specify the width of the plot:
Specify the height of the plot:
Allow the width and height to be up to a certain size:
Specify the width and height for a graphic, padding with space if necessary:
Setting AspectRatioFull will fill the available space:
Use maximum sizes for the width and height:
Use ImageSizeFull to fill the available space in an object:
Specify the image size as a fraction of the available space:
PerformanceGoal (2)
PlotLegends (4)
Add a color bar for the different values:
PlotLegends automatically picks up Contours and ContourShading values:
With the setting ContourShadingAutomatic, the colors are derived from ColorFunction:
Control placement of the legend with Placed:
PlotRange (3)
PlotTheme (3)
Use a theme with detailed grid lines, ticks, and legends:
Any option setting overrides PlotTheme settings, in this case removing face grids:
ScalingFunctions (5)
By default, plots have linear scales in all directions:
Create a plot with a log-scaled ![]() axis:
axis:
Use ScalingFunctions to scale to reverse the coordinate direction in the ![]() direction:
direction:
Use a scale defined by a function and its inverse:
Slice surfaces that are defined relative to the bounding box are unaffected by scaling functions:
TargetUnits (2)
Axes and legends are labeled with the units specified by TargetUnits:
Units specified by Quantity are converted to those specified by TargetUnits:
Ticks (6)
Ticks are placed automatically in each plot:
Use TicksNone to not draw any tick marks:
Place tick marks at specific positions:
Draw tick marks at the specified positions with the specified labels:
Specify tick marks with scaled lengths:
Customize each tick with position, length, labeling and styling:
TicksStyle (3)
Applications (17)
Elementary Functions (4)
Distribution Functions (6)
Plot the PDF of a distribution:
Simulate the distribution and show point distribution:
Plot the CDF of a distribution:
The SurvivalFunction:
The HazardFunction:
Explore Correlation parameters for a MultinormalDistribution, where ρab is the correlation between a and b:
Correlation between x and y only:
Correlation between y and z only:
Correlation between y and z only, but larger variance ![]() in the z component:
in the z component:
Visualize the PDF of a ProductDistribution:
A product of three different distributions:
A product of bivariate and univariate distributions:
Plot the pdf of a CopulaDistribution:
Visualize the PDF of a kernel density estimate of some trivariate data:
Potential and Wave Functions (4)
Plot the phase using color on the isosurface of a quadrupole potential:
Alternatively, show the ![]() on several planes:
on several planes:
Plot spherical waves ![]() from three sources
from three sources ![]() in space:
in space:
Plot hydrogen orbital densities for quantum numbers ![]() ,
, ![]() ,
, ![]() :
:
An electrostatic potential built from a collection of point charges ![]() at positions
at positions ![]() :
:
Partial Differential Equations (3)
Visualize a nonlinear sine-Gordon equation in two spatial dimensions with periodic boundary conditions with time represented along the z axis:
The solution evolves in time along the z axis:
Visualize Wolfram's nonlinear wave equation in two spatial dimensions with time represented along the z axis:
Visualize solutions to 3D partial differential equations. In this case, a Poisson equation over a Ball and Dirichlet boundary conditions:
Properties & Relations (5)
Use SliceDensityPlot3D for continuous densities on surfaces:
Use ContourPlot3D for constant value surfaces:
Use DensityPlot3D for full volume visualization of the function values:
Use ListSliceContourPlot3D for data:
Use ContourPlot for contour plots in 2D:
See Also
ListSliceContourPlot3D SliceDensityPlot3D ContourPlot ContourPlot3D
Function Repository: SectionParametricPlot3D SectionPlot3D SectionContourPlot
Related Guides
Text
Wolfram Research (2015), SliceContourPlot3D, Wolfram Language function, https://reference.wolfram.com/language/ref/SliceContourPlot3D.html (updated 2022).
CMS
Wolfram Language. 2015. "SliceContourPlot3D." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/SliceContourPlot3D.html.
APA
Wolfram Language. (2015). SliceContourPlot3D. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SliceContourPlot3D.html
BibTeX
@misc{reference.wolfram_2025_slicecontourplot3d, author="Wolfram Research", title="{SliceContourPlot3D}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/SliceContourPlot3D.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_slicecontourplot3d, organization={Wolfram Research}, title={SliceContourPlot3D}, year={2022}, url={https://reference.wolfram.com/language/ref/SliceContourPlot3D.html}, note=[Accessed: 25-February-2026]}