Catalytic Converter
| Introduction | Initial and Boundary Conditions |
| Mass Transport Model | Solve the PDE Model |
| Domain | Post-processing and Visualization |
| Flow Regime | Nomenclature |
Introduction
A catalytic converter is an emission control device that reduces certain pollutants in exhaust gas from an internal combustion engine. With the assistance of catalysts, molecules such as nitric oxide, ![]() , and carbon monoxide,
, and carbon monoxide, ![]() , can be oxidized and converted to substances that are somewhat less harmful to the environment.
, can be oxidized and converted to substances that are somewhat less harmful to the environment.
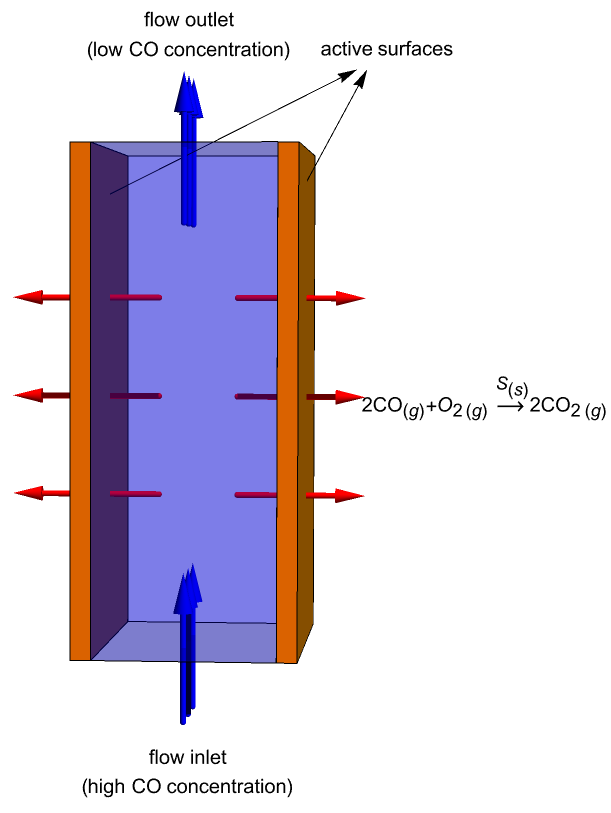
This study is to simulate mass transportation of ![]() molecules within a catalytic converter and their evolution in time. The catalytic converter modeled in this example consists of two parallel plates (active surfaces) with a catalyst
molecules within a catalytic converter and their evolution in time. The catalytic converter modeled in this example consists of two parallel plates (active surfaces) with a catalyst ![]() on them. A gas containing
on them. A gas containing ![]() molecules enters the domain from the bottom, flows across the reacting plates and then exits the converter through the top. During this process, the
molecules enters the domain from the bottom, flows across the reacting plates and then exits the converter through the top. During this process, the ![]() molecules near the plates are continuously oxidized into carbon dioxide:
molecules near the plates are continuously oxidized into carbon dioxide:
In the Post-Processing section, the converter performance will be measured by calculating the net reduction in the ![]() concentration
concentration ![]() between the flow inlet
between the flow inlet ![]() and outlet
and outlet ![]() :
:
For this, the mean ![]() concentration at the boundary
concentration at the boundary ![]() is computed with a boundary integration using NIntegrate:
is computed with a boundary integration using NIntegrate:
The catalytic converter model is built and solved from time ![]() to
to ![]() . Then it will be determined when the system reaches its steady state.
. Then it will be determined when the system reaches its steady state.
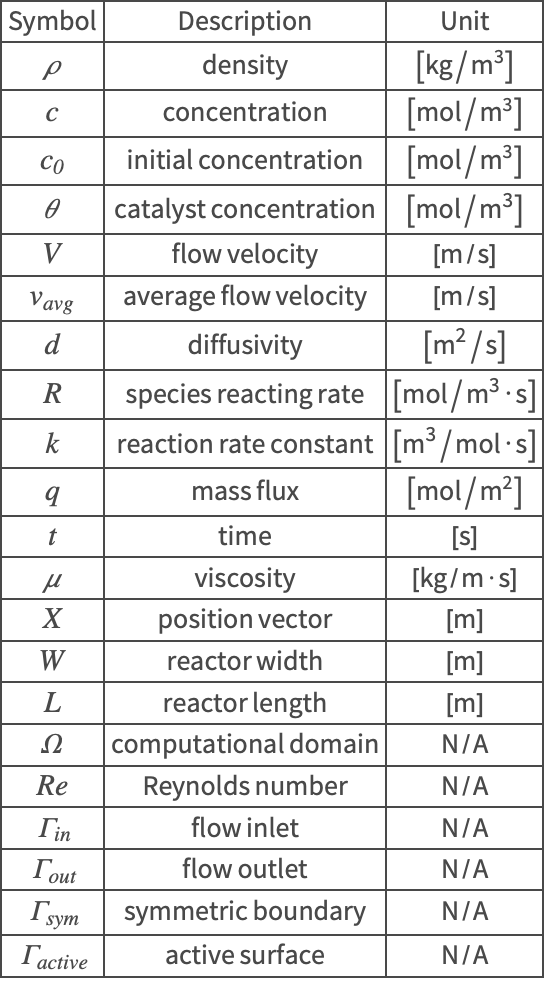
The symbols and corresponding units used here are summarized in the Nomenclature section.
Please refer to the information provided in the "Mass Transport" tutorial for a more general theoretical background for heat transfer analysis.
Mass Transport Model
The conservative transport equation (1), which is derived from mass conservation, is used to solve for the concentration distribution ![]() in a mass transport model:
in a mass transport model:
Here:![]() is the concentration of the transported species
is the concentration of the transported species ![]() ,
,![]() is the species diffusivity
is the species diffusivity ![]() ,
,![]() is the velocity field of possible flow inside the medium
is the velocity field of possible flow inside the medium ![]() ,
,![]() is the mass production/consumption, the volumetric reacting rate of the species
is the mass production/consumption, the volumetric reacting rate of the species ![]() .
.
In this model, the reaction of the carbon monoxide, ![]() , takes place on the active surfaces only and will be modeled with a mass flux boundary condition. Since no other reaction occurs within the converter, the volumetric reacting rate
, takes place on the active surfaces only and will be modeled with a mass flux boundary condition. Since no other reaction occurs within the converter, the volumetric reacting rate ![]() is set to zero, and the transport equation simplifies to:
is set to zero, and the transport equation simplifies to:
Domain
The catalytic converter model consists of two parallel reacting plates. If the depth of the plates is reasonably longer than their length and width, then the variation of ![]() concentration in the
concentration in the ![]() direction can be neglected. Therefore, a two-dimensional model is sufficient to represent the 3D reactor.
direction can be neglected. Therefore, a two-dimensional model is sufficient to represent the 3D reactor.
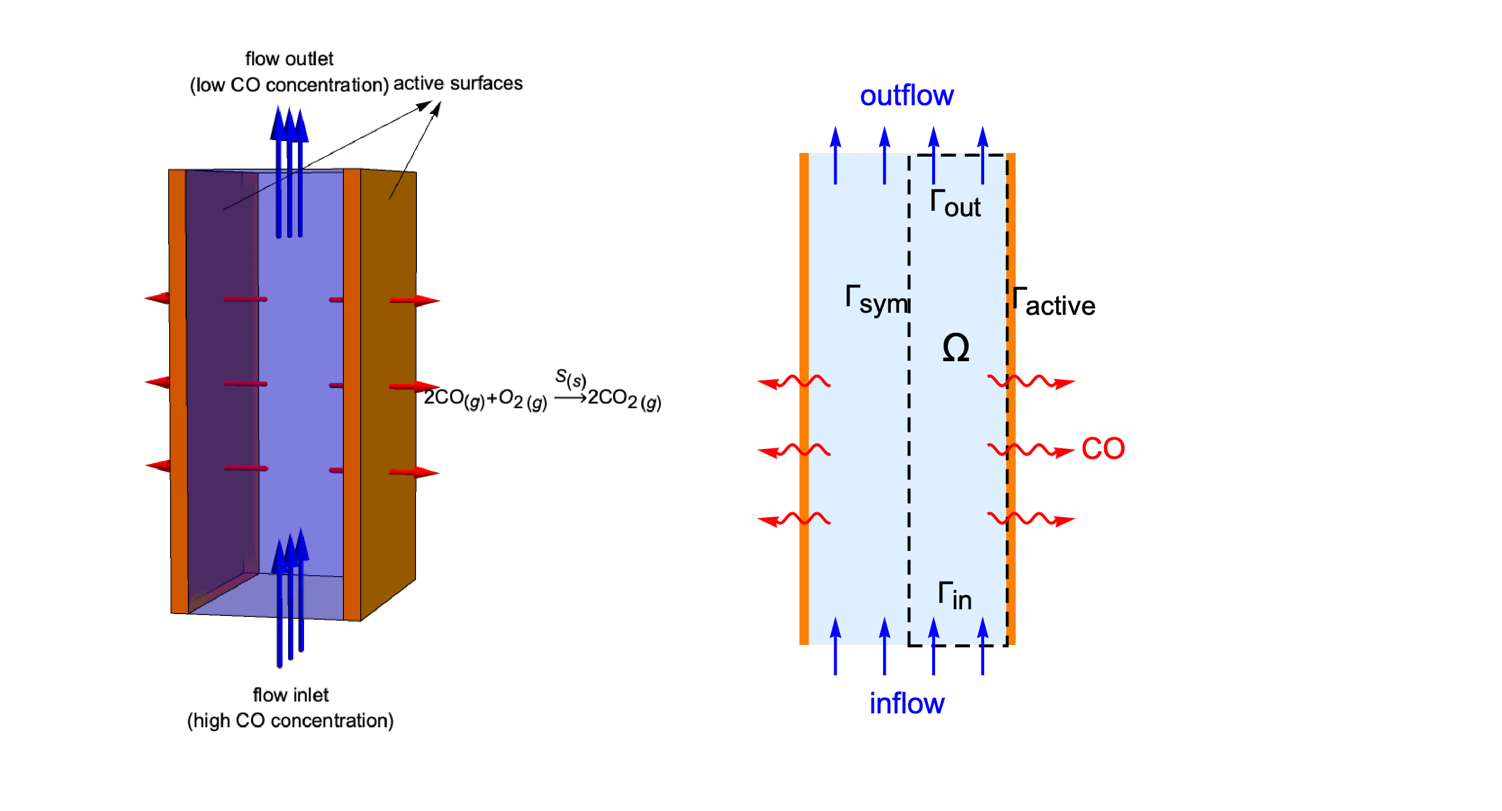
Due to the symmetry along the ![]() axis, it is effective to only make use of the right half of the reactor as the simulation domain
axis, it is effective to only make use of the right half of the reactor as the simulation domain ![]() . Here,
. Here, ![]() and
and ![]() denote the flow inlet and flow outlet. The active surface and the symmetric boundary are symbolized as
denote the flow inlet and flow outlet. The active surface and the symmetric boundary are symbolized as ![]() and
and ![]() , respectively:
, respectively:
Flow Regime
In this model, the exhausted gas is flowing through the reactor at an average velocity of ![]() . To determine whether the gas flow is laminar or turbulent, inspect the Reynolds number within the domain:
. To determine whether the gas flow is laminar or turbulent, inspect the Reynolds number within the domain:
Here, the density and the viscosity of the gas flow are given by ![]() and
and ![]() , respectively. The characteristic length is taken as the length of the reactor
, respectively. The characteristic length is taken as the length of the reactor ![]() .
.
Empirically, the flow is considered as laminar when ![]() and as turbulent when
and as turbulent when ![]() .
.
Therefore, the flow velocity ![]() within the reactor can be determined by the analytical laminar profile:
within the reactor can be determined by the analytical laminar profile:
Initial and Boundary Conditions
At the beginning of the simulation, the carbon monoxide is uniformly distributed in the converter with an initial concentration ![]() .
.
There are four types of boundary conditions involved in this mass transport model. At the flow inlet, the ![]() concentration is held fixed at
concentration is held fixed at ![]() . There is an infinite supply of
. There is an infinite supply of ![]() behind the inlet.
behind the inlet.
At the top boundary, an outflow boundary condition is used to model the flow outlet where ![]() molecules are transported out of the domain.
molecules are transported out of the domain.
On the active surface, the carbon monoxide is absorbed and transformed by the catalyst ![]() and can be modeled by a mass flux boundary condition:
and can be modeled by a mass flux boundary condition:
Here, the mass flux ![]() denotes the absorption rate of
denotes the absorption rate of ![]() molecules and is proportional to its own concentration
molecules and is proportional to its own concentration ![]() , the concentration of the remaining catalyst sites
, the concentration of the remaining catalyst sites ![]() and the reaction rate constant
and the reaction rate constant ![]() :
:
Assuming that each carbon monoxide molecule occupies exactly one catalyst site during the reaction, then the concentration of remaining sites, ![]() , is equal to the difference between the total concentration of active sites,
, is equal to the difference between the total concentration of active sites, ![]() , and the number of sites occupied by the absorbed carbon monoxide:
, and the number of sites occupied by the absorbed carbon monoxide:
A default symmetric boundary condition is implicitly applied on the symmetric boundary ![]() .
.
Solve the PDE Model
To analyze the transport of ![]() molecules and their evolution in time, the PDE model is solved from
molecules and their evolution in time, the PDE model is solved from ![]() to
to ![]() .
.
Post-processing and Visualization
First, to inspect the effect of the catalytic converter, the ![]() concentration
concentration ![]() evolving in time is visualized.
evolving in time is visualized.
See this note about improving the visual quality of the animation.
With the presence of the catalyst ![]() ,
, ![]() molecules near the right boundary (active surface) are continuously absorbed and converted into carbon dioxide, resulting in a layer-like concentration field. The thickness of this concentration layer grows with time and reaches its steady state around
molecules near the right boundary (active surface) are continuously absorbed and converted into carbon dioxide, resulting in a layer-like concentration field. The thickness of this concentration layer grows with time and reaches its steady state around ![]() .
.
Since the ![]() concentration has little variation outside this layer, it is known as the "reaction dead space". To minimize the reaction dead space and improve the overall converting effectiveness, the catalyst converter is often made in a shape of honeycombs rather than parallel plates.
concentration has little variation outside this layer, it is known as the "reaction dead space". To minimize the reaction dead space and improve the overall converting effectiveness, the catalyst converter is often made in a shape of honeycombs rather than parallel plates.
To determine the exact time when the system reaches the steady state, WhenEvent can be used to check whether the concentration field ![]() has converged within the pre-defined threshold.
has converged within the pre-defined threshold.
In this case, the system is said to be in steady state once the concentration derivative is below ![]() :
:
To see how the ![]() molecules vary in the flow direction, the concentration is plotted along the vertical line
molecules vary in the flow direction, the concentration is plotted along the vertical line ![]() .
.
Note that the curves for ![]() ,
, ![]() and
and ![]() are almost overlapping, which means the system has already reached its steady state.
are almost overlapping, which means the system has already reached its steady state.
To measure the effectiveness of the catalytic converter, the net ![]() reduction is calculated between the flow inlet
reduction is calculated between the flow inlet ![]() and outlet
and outlet ![]() . For this, the mean concentration at the boundary
. For this, the mean concentration at the boundary ![]() is computed with a boundary integration:
is computed with a boundary integration:
Note that the two values are nearly the same, which confirms that the system has reached its steady state after ![]() .
.
With the catalytic converter, the concentration of the carbon monoxide ![]() has been reduced by
has been reduced by ![]() .
.