AASTriangle

AASTriangle[α,β,a]

returns a filled triangle with angles α and β and side length a, where a is adjacent to one angle only.

Details and Options

  • AASTriangle is also known as angle-angle-side triangle.
  • AASTriangle can be used as a primitive in 2D graphics and as a geometric region in 2D.
  • The given (blue) and computed (red) parameters for an AASTriangle:
  • AASTriangle returns a Triangle with 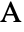at the origin, 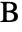on the positive 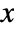axis, and 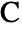in the half-plane .
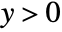  • AASTriangle allows the length a to be any positive number and the angles α and β to be positive such that α+β<π.

Background & Context

  • AASTriangle constructs an angle-angle-side triangle. In particular, AASTriangle[α,β,a] returns the Triangle in TemplateBox[{}, Reals]^2 with vertices 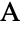, 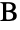and 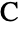located at the origin, on the positive 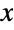axis and in the upper half-plane, respectively, with α∠BAC, β∠ABC and a the length of the side opposite 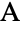. By the AAS theorem, the triangle so specified is unique (up to geometric congruence). AASTriangle allows the length a to be any positive number and the angles α and β to be positive numbers satisfying α+β<π. The arguments of AASTriangle may be exact or approximate numeric expressions.
  • The Triangle objects returned by AASTriangle can be used as 2D graphics primitives or geometric regions.
  • AASTriangle is related to a number of other symbols. ASATriangle, SASTriangle and SSSTriangle return two-dimensional triangles constructed using different angle and/or side specifications. Finally, AASTriangle is a special case of Triangle, in the sense that AASTriangle[α,β,a] is equivalent to Triangle[{{0,0},{a Csc[α] Sin[α+β],0},{a Cot[α] Sin[β],a Sin[β]}}].

Examples

open allclose all

Basic Examples  (4)

A triangle with , , and :

An AASTriangle:

Different styles applied to AASTriangle:

Area and centroid:

Centroid:

Scope  (14)

Graphics  (4)

Specification  (2)

AASTriangle evaluates to Triangle with one point at the origin and one edge on the axis:

A triangle with a symbolic angle:

Plot them:

Styling  (2)

Color directives specify the face color:

FaceForm and EdgeForm can be used to specify the styles of the interior and boundary:

Regions  (10)

Embedding dimension is the dimension of the space in which the triangle lives:

Geometric dimension is the dimension of the triangle itself:

Membership testing:

Conditions for membership:

Area:

Centroid:

Distance from a point to an AASTriangle:

Visualize it:

Signed distance from a point:

Nearest point:

Visualize it:

A triangle is bounded:

Find its range:

Integrate over an AASTriangle:

Optimize over it:

Solve equations over an AASTriangle:

Applications  (2)

A triangle with two equal angles is an isosceles triangle:

Visualize it:

Find the area:

The circumcircle of an AASTriangle can be found using Circumsphere:

The circumcircle passes through the three corner points:

Find the midpoints for each edge of the triangle:

The perpendicular bisectors are lines from the circumcenter to the midpoints:

Properties & Relations  (2)

AASTriangle is a specialized case of Triangle:

Any AASTriangle can be represented by a Polygon:

Neat Examples  (1)

Varying an angle:

Wolfram Research (2014), AASTriangle, Wolfram Language function, https://reference.wolfram.com/language/ref/AASTriangle.html.

Text

Wolfram Research (2014), AASTriangle, Wolfram Language function, https://reference.wolfram.com/language/ref/AASTriangle.html.

CMS

Wolfram Language. 2014. "AASTriangle." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AASTriangle.html.

APA

Wolfram Language. (2014). AASTriangle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AASTriangle.html

BibTeX

@misc{reference.wolfram_2024_aastriangle, author="Wolfram Research", title="{AASTriangle}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/AASTriangle.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_aastriangle, organization={Wolfram Research}, title={AASTriangle}, year={2014}, url={https://reference.wolfram.com/language/ref/AASTriangle.html}, note=[Accessed: 22-November-2024 ]}