AdjacencyMatrix

AdjacencyMatrix[g]

グラフ g の頂点 - 頂点の隣接行列を与える．

AdjacencyMatrix[{vw,…}]

規則 vw を使ってグラフ g を指定する．

詳細

  • 隣接行列は，連結性行列としても知られている．
  • AdjacencyMatrixはNormalを使って通常の行列に変換可能なSparseArrayオブジェクトを返す．
  • 隣接行列の項 aijは頂点 νiから頂点 νjへの有向辺の数である．
  • 対角項 aiiは頂点 viのループの数を数える．
  • 無向辺は方向が逆の2つの有向辺と解釈される．
  • 頂点 viはVertexList[g]で与えられる順序であるとみなされる．
  • グラフの隣接行列の次元は 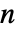× 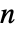である．ただし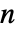， は頂点数である．

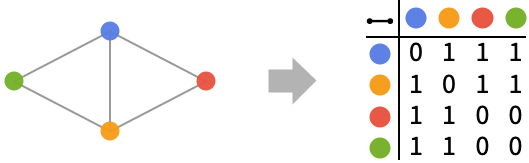
予備知識

  • AdjacencyMatrixは，正方行列を返す．その行と列はグラフの頂点に対応し，要素 aij は，頂点 vi から頂点 vj までの（有向）辺の数を与える非負の整数である．隣接行列は，行列に対する簡単な操作を使って，数多くの特性を計算するのに使えるグラフの便利な表現を提供する．隣接行列を与えることによって効率的に行えるグラフの計算の例には，頂点次数，入次数と出次数，最高で 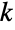ステップの頂点間の経路の数，グラフスペクトル等がある．
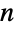  • 個の頂点のグラフについては，隣接行列は 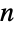× 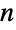の次元を持つ．無向グラフについては，隣接行列は対称である．有限の単純グラフ（例：自己ループや複数辺を持たない，無向で，重みなしのグラフ）については，隣接行列は対角に0を持たなければならず，その行列要素は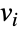， が 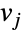に隣接している場合には 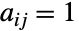によって，その他の場合には 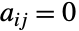によって与えられる．
  • 頂点の特定の順序に基づくグラフの明示的な隣接行列の表現は，一意的である．しかし，グラフの頂点は置換できるので，対応する同形クラスのグラフを表す隣接行列のクラスが存在する．ただし，同形クラスの隣接行列は行列の行と列の一意的なモジュロ置換である（グラフ頂点のラベルを付け直すことに正確に対応する）．
  • AdjacencyGraphを使って，隣接行列からグラフを構築することができる．IncidenceMatrixは，頂点と頂点の関係の代りに，頂点と辺の関係を与えるグラフの別の行列表現を与える．AdjacencyMatrixはグラフの重みを考慮に入れないので，辺の重みを持つグラフの隣接行列を計算する場合には，WeightedAdjacencyMatrixを使わなければならない．

例題

すべて開くすべて閉じる

例  (2)

無向グラフの隣接行列：

有向グラフの隣接行列：

スコープ  (5)

無向グラフの隣接行列は対称である：

有向グラフの隣接行列は対称ではない：

規則を使ってグラフを指定する：

自己ループがあるグラフの隣接行列には対角項がある：

AdjacencyMatrixは大きいグラフに使うことができる：

MatrixPlotを使って行列を可視化する：

アプリケーション  (7)

隣接行列から無向グラフの次数を計算する：

有向グラフの入次数をその隣接行列から計算する：

有向グラフの出次数をその隣接行列から計算する：

有向グラフのすべての頂点間の厳密に ステップまでの経路数を数える：

1から5へのステップ2の経路が2本ある：

有向グラフで から までの厳密にステップ の経路の数を数える：

2つの頂点の共引用が共通祖先の数である共引用行列を計算する：

と の間の共引用：

2つの頂点間のカップリングが共通祖先の数であるカップリング行列を計算する：

と の間のカップリング：

特性と関係  (14)

隣接行列の行と列はVertexListで与えられる順序に従う：

VertexIndexを使って頂点ペアに対応する行列の行と列を求める：

1と4が隣接頂点かどうか調べる：

EdgeQと比較する：

無向グラフには対称隣接行列がある：

AdjacencyGraphを使って隣接行列からグラフを構築する：

ループのない任意のグラフの隣接行列の主対角の項はすべて0である：

隣接行列の行と列の数は頂点数に一致する：

同型グラフが異なる隣接行列を持つことがある：

g の隣接行列を等しい h の行列を得るマッピングに従って置換する：

d 固有値の多重性が1であるとき，d 正則グラフ g は連結グラフである：

このグラフは3-正則である：

3の多重性が1なのでこれは連結グラフである：

完全グラフの場合は，対角外の項はすべて隣接行列では1である：

完全 部グラフの対角ブロックの項は0である：

TuranGraphは二部グラフである：

StarGraphは第1行と第1列のみに1がある：

経路グラフの隣接行列の行には1つか2つの項がある：

線グラフの隣接行列はそのIncidenceMatrixで計算することができる：

考えられる問題  (1)

空グラフには隣接行列はない：

Wolfram Research (2010), AdjacencyMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/AdjacencyMatrix.html （2015年に更新）.

テキスト

Wolfram Research (2010), AdjacencyMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/AdjacencyMatrix.html （2015年に更新）.

CMS

Wolfram Language. 2010. "AdjacencyMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/AdjacencyMatrix.html.

APA

Wolfram Language. (2010). AdjacencyMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AdjacencyMatrix.html

BibTeX

@misc{reference.wolfram_2024_adjacencymatrix, author="Wolfram Research", title="{AdjacencyMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/AdjacencyMatrix.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_adjacencymatrix, organization={Wolfram Research}, title={AdjacencyMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/AdjacencyMatrix.html}, note=[Accessed: 22-November-2024 ]}