AnglePath3D
AnglePath3D[{{α1,β1,γ1},{α2,β2,γ2},…}]
{0,0,0}から始まり,それぞれがオイラー角 αi,βi,γiによるオブジェクトの連続的な回転の結果である ![]() 軸方向に単位長の一連のステップを取る,オブジェクトの経路の3D座標のリストを与える.
軸方向に単位長の一連のステップを取る,オブジェクトの経路の3D座標のリストを与える.
AnglePath3D[{{α1,β1},{α2,β2},…}]
オイラー角 γiが0であると仮定する.
AnglePath3D[{mat1,mat2,…}]
連続する回転が3D回転行列 matiで指定されるとみなす.
AnglePath3D[{{r1,rot1},{r2,rot2},…}]
rotiで指定されたオイラー角あるいは回転行列で長さ riの連続するステップを取る.
AnglePath3D[{x0,y0,z0},steps]
点{x0,y0,z0}から開始する.
AnglePath3D[{rot0},steps]
オイラー角または回転行列 rot0に従ってオブジェクトを回転させることで指定された ![]() 軸方向に進む.
軸方向に進む.
AnglePath3D[{{x0,y0,z0},rot0},steps]
rot0で指定された ![]() 軸方向で点{x0,y0,z0}から開始する.
軸方向で点{x0,y0,z0}から開始する.
AnglePath3D[init,steps,form]
各ステップで,form で指定された形のデータを返す.
詳細とオプション


- AnglePath3Dが連続的に取る方向は,連続する局所フレームの
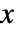 軸で決定される.これは,3Dオブジェクの向きを定義すると考えることができる.
軸で決定される.これは,3Dオブジェクの向きを定義すると考えることができる. - デフォルトで,初期フレームの向きは座標軸と揃っている.
- 各ステップで,局所フレームは回転され,経路は新たなフレーム内で指定された距離だけ
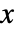 軸に沿って進む.
軸に沿って進む. - 3つ一組の角度{αi,βi,γi}は,一般に,オイラーの回転行列EulerMatrix[{αi,βi,γi},{3,2,1}]に等しい.この表記法では,αiは経度角, βiは緯度角,γiは変位軸の周りの回転角である.
- ステップ長は{{r1,rot1},{r2,rot2},…}で,あるいは同様に{{r1,r2,…},{rot1,rot2,…}}で指定することができる.
- 方向が matiで指定された長さ riのステップについては,次の位置 pi={xi,yi,zi}を pi=pi-1+fi.{ri,0,0}で得ることができる.フレームの回転行列 fiは fi=fi-1.matiおよび f0=mat0で与えられる.
- AnglePath3D[steps,form]はAnglePath3D[{0,0,0},steps,form]に等しい.
- AnglePath3D[…,form]の form は以下から選ぶことができる.
-
"Position" 直交座標{xi,yi,zi}(デフォルト) "FrameMatrix" フレーム fiの f0に対する回転行列 "EulerMatrix" フレーム fiのフレーム fi - 1に対する回転行列 "FrameAngles" EulerAngles[fi,{3,2,1}] "EulerAngles" {αi,βi,γi} "Translation" TranslationTransform[{xi,yi,zi}] "Rotation" AffineTransform[fi] "RotationTranslation" AffineTransform[{fi,{xi,yi,zi}}] {form1,form2,…} 形のリスト - 引数 init および steps は記号的でもよく,Quantityオブジェクトでもよい.
- AnglePath3DにはオプションWorkingPrecisionがある.このオプションは生成する数の精度を決定する.
- デフォルト設定のWorkingPrecisionAutomaticでは,短いパスに対してのみ厳密な入力に対して厳密数が生成される.パスが長くなると機械精度が使われる.
例題
すべて開くすべて閉じる例 (6)
スコープ (22)
ステップ指定 (7)
![]() 軸の方向に位置{0,0,0}から始まる3つの角が1組みになったオイラー角で単位ステップの経路を生成する:
軸の方向に位置{0,0,0}から始まる3つの角が1組みになったオイラー角で単位ステップの経路を生成する:
AnglePath3D[{{α1,β1},{α2,β2},…}]は,3番目のオイラー角が0であると仮定する:
ステップの長さと方向は,繋げて与えることも別々に与えることもできる:
入力でQuantityオブジェクトを使う:
経路の初期化 (7)
データの形式 (8)
デフォルトで,AnglePath3Dは各ステップで到達した点の位置を返す:
大域的フレーム内の各局所フレームの向きを決定するオイラー角を計算する:
1回のAnglePath3Dの呼出しでデータのさまざまな形を生成する:
オプション (1)
WorkingPrecision (1)
デフォルトで,AnglePath3Dはパスが短いときは厳密な入力に対しては厳密数を与え,パスが長くなると機械数を与える:
アプリケーション (7)
特性と関係 (5)
AnglePath3D[{{θ1,0,0},{θ2,0,0},…}]は ![]() -
-![]() 平面上の経路を返す:
平面上の経路を返す:
生成された経路はAnglePath[{θ1,θ2,…}]の経路と等しい:
オイラー角を指定することは ![]() -
-![]() -
-![]() オイラー行列を指定することに等しい:
オイラー行列を指定することに等しい:
初期オイラー角を指定することは,初期 ![]() -
-![]() -
-![]() オイラー行列を指定することに等しい:
オイラー行列を指定することに等しい:
インタラクティブな例題 (1)
テキスト
Wolfram Research (2017), AnglePath3D, Wolfram言語関数, https://reference.wolfram.com/language/ref/AnglePath3D.html (2019年に更新).
CMS
Wolfram Language. 2017. "AnglePath3D." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/AnglePath3D.html.
APA
Wolfram Language. (2017). AnglePath3D. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AnglePath3D.html