Annulus

Annulus[{x,y},{rinner,router}]

{x,y}を中心とする，内半径 rinner，外半径 routerのアニュラスを表す．

Annulus[{x,y},{rinner,router},{θ1,θ2}]

角度 θ1から θ2までのアニュラスを表す．

詳細とオプション

  • Annulusは，穴あき円板としても知られている．
  • Annulusは，幾何学領域およびグラフィックスプリミティブとして使うことができる．
  • Annulus[]はAnnulus[{0,0},{1/2,1}]に等しい．
  • Annulus[r]はAnnulus[{0,0},{r/2,r}]に等しい．
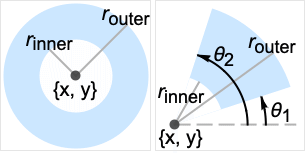
  • Annulus[{rinner,router}]はAnnulus[{0,0},{rinner,router}]に等しい．
  • Annulusは，塗り潰された領域{p|r_(inner)<=TemplateBox[{{p, -, {{, {x, ,, y}, }}}}, Norm]<=r_(outer)}あるいは{p|r_(inner)<=TemplateBox[{{p, -, {{, {x, ,, y}, }}}}, Norm]<=r_(outer)} intersection Disk[{x,y},r_(outer),{theta_1,theta_2}]を表す．
  • Annulusは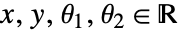，および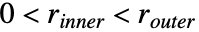を許容する．
  • 角度は，正の x 方向からラジアン単位で反時計回りに測られる．
  • AnnulusはGraphicsで使うことができる．
  • グラフィックスでは，{xi,yi}はDynamic式でよい．
  • グラフィックスの描画は，FaceForm，EdgeForm等の指示子および色の影響を受ける．

例題

すべて開くすべて閉じる

例  (4)

標準的なアニュラス：

アニュラスの一部：

さまざまなスタイルのアニュラス：

アニュラスのAreaを求める：

アニュラスのスライスの面積：

スコープ  (17)

グラフィックス  (7)

指定  (4)

半径を指定する：

中心を指定する：

アニュラスの一部：

原点における基本的なアニュラスの短縮形：

スタイリング  (2)

色指示子で各アニュラスの表面色を指定する：

FaceFormおよびEdgeFormを使って内部と境界のスタイルを指定することができる：

アニュラスの境界：

座標  (1)

点はDynamicでよい：

領域  (10)

埋込み次元：

幾何次元：

点の帰属判定：

点の帰属条件を得る：

面積：

重心：

点からの距離：

基本的なアニュラス内の最近点までの距離：

点からの符号付き距離：

基本的アニュラスまでの符号付き距離：

領域内の最近点：

最近点：

アニュラスは有界である：

範囲を求める：

アニュラス上で積分する：

アニュラス上で最適化する：

アニュラス内で方程式を解く：

アプリケーション  (4)

アニュラスの上で関数をプロットする：

コンデンサは基本的に間に絶縁体が入った導体平板のペアである．コンデンサの電気容量は板の分離と重なり合う面積の関数で，このことから，重なり合う部分を変えるために回転させることができる半アニュラスの集合から作ることができる可変コンデンサを作ることができる．接続している2つのアニュラスの重なり合う部分の弧を与える関数を作る：

次に重なり合う面積を求める関数を作る：

であるので，電気容量を計算する関数を作ることができる：

インタラクティブでグラフィカルな容量（単位：ピコファラッド）を表示する可変コンデンサの表現形を作ることができる：

木の成長につれて，その年の気候によって断面にさまざまな太さの年輪が見られる．アニュラスを使って年輪に似たパターンを作ることができる．まず，ランダムではあるが隣接した内半径と外半径のリストを生成する：

ランダムな色（茶系）を使って同心円のアニュラスの表を作成する：

最後に，最小のアニュラスの内半径と半径が等しい円板を中心としてすべてのアニュラスを可視化する：

ある種の条件下で金環日食が起こることがある．「アニュラス（環）」の語は，空に浮かぶ太陽と月の相対的な大きさのため，太陽の一部（コロナ）が月の周りに見えて明るい環を形成するところからきている．この現象のインタラクティブなデモンストレーションを作り，金環日食時に明るい白の環を作ることができる：

特性と関係  (6)

Diskは，が0に近付く際のAnnulusの極限である：

Circleは が に近付く際のAnnulusの極限である：

アニュラスは2つの同心Disk領域間のRegionDifferenceの閉包である：

ImplicitRegionは任意のAnnulusを表すことができる：

ParametricRegionはAnnulusを表すことができる：

Annulusは，半径の円から未満の点である：

おもしろい例題  (3)

ランダムなアニュラスの集合：

アニュラスの族：

デジタル花弁：

Wolfram Research (2015), Annulus, Wolfram言語関数， https://reference.wolfram.com/language/ref/Annulus.html.

テキスト

Wolfram Research (2015), Annulus, Wolfram言語関数， https://reference.wolfram.com/language/ref/Annulus.html.

CMS

Wolfram Language. 2015. "Annulus." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Annulus.html.

APA

Wolfram Language. (2015). Annulus. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Annulus.html

BibTeX

@misc{reference.wolfram_2024_annulus, author="Wolfram Research", title="{Annulus}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/Annulus.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_annulus, organization={Wolfram Research}, title={Annulus}, year={2015}, url={https://reference.wolfram.com/language/ref/Annulus.html}, note=[Accessed: 22-November-2024 ]}