WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

Sphere
✖
Sphere

✖
Sphere[p]

represents a unit sphere centered at the point p.

✖
Sphere[p,r]

represents a sphere of radius r centered at the point p.

✖
Sphere[{p1,p2,…},r]

represents a collection of spheres of radius r.

Details and Options

  • Sphere can be used as a geometric region and a graphics primitive.
  • Sphere[] is equivalent to Sphere[{0,0,0}]. »
  • Sphere[n] for positive integer n is equivalent to Sphere[{0,…,0}], a unit sphere in .
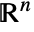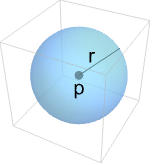
  • Sphere represents the shell {x|TemplateBox[{{x, -, p}}, Norm]=r}.
  • Sphere can be used in Graphics and Graphics3D.
  • In graphics, the points p, pi and radii r can be Scaled and Dynamic expressions.
  • Graphics rendering is affected by directives such as FaceForm, Specularity, Opacity, and color.
  • Sphere[{p1,p2,…},{r1,r2,…}] represents a collection of spheres with centers pi and radii ri.

Background & Context

  • Sphere is a graphics and geometry primitive that represents a sphere in 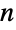-dimensional space. In particular, Sphere[p,r] represents the sphere {x:TemplateBox[{{x, -, p}}, Norm]=r} in TemplateBox[{}, Reals]^n with center p and radius r, where r may be any non-negative real number and p can have any positive length 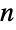. The shorthand form Sphere[p] is equivalent to Sphere[p,1] and Sphere[n] is equivalent to Sphere[ConstantArray[0, n],1], while Sphere[] autoevaluates to Sphere[{0,0,0}].
  • Collections of sphere objects (multi-spheres) of common radius 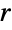may be efficiently represented using Sphere[{p1,…,pk},r] and balls of varying radii represented using Sphere[{p1,…,pk},{r1,…,rk}].
  • Sphere objects can be visually formatted in two and three dimensions using Graphics and Graphics3D, respectively. The appearance of Sphere objects in graphics can be modified by specifying the face directive FaceForm (in 3D); color directives such as Red; the transparency and specularity directives Opacity and Specularity; and the style option Antialiasing.
  • Sphere may also serve as a region specification over which a computation should be performed. For example, Integrate[1,{x,y,z}∈Sphere[{0,0,0},r]] and Area[Sphere[{0,0,0},r]] both return the surface area 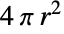of a sphere of radius .
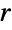  • Sphere is related to a number of other symbols. Sphere represents the boundary of a ball, as can be computed using RegionBoundary[Ball[{x,y,z},r]]. Ellipsoidal surfaces (not to be confused with the solid ellipsoids represented by Ellipsoid) may be obtained from a Sphere using Scaled. A sphere passing through a set of given points may be obtained using Circumsphere. Sphere objects may be represented as ImplicitRegion[(x-u)2+(y-v)2+(z-w)2r2,{u,v,w}] or ParametricRegion[{x,y,z}+r{Cos[θ]Sin[ϕ],Sin[θ]Sin[ϕ],Cos[ϕ]},{{θ,0,2π},{ϕ,0,π}}]. Precomputed properties of the sphere in standard position are available using SurfaceData["Sphere",property] or Entity["Surface","Sphere"][property].

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

A unit sphere at the origin:

In[3]:=3
✖
https://wolfram.com/xid/0y7yz6-c7o
Out[1]=1

Area and centroid:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-7wedhk
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-kxw6nj
Out[2]=2

Scope  (22)Survey of the scope of standard use cases

Graphics  (12)

Specification  (4)

A unit sphere:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-btz1q2
Out[1]=1

Spheres with different radii:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-l0hn2
Out[1]=1

Short form for a unit sphere at the origin:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-37iz6
Out[1]=1

Multiple spheres:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-mlyae
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-k7s9me
Out[2]=2

Styling  (4)

Colored spheres:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-cdxdbh
Out[1]=1

Different properties can be specified for the front and back of faces using FaceForm:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-vb6wx
Out[1]=1

Spheres with different specular exponents:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-d1tyd0
Out[1]=1

Black sphere that glows red:

In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-ca9zt
Out[2]=2

Opacity specifies the face opacity:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-v6995
Out[1]=1

Coordinates  (4)

Use Scaled coordinates:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-d1y67i
Out[1]=1

Use Scaled radius:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-ek3mgx
Out[1]=1

Specify scaled offsets from the ordinary coordinates:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-nn6a0g
Out[1]=1

Points can be Dynamic:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-6gl1zz
Out[1]=1

Regions  (10)

Embedding dimension is the dimension of the space in which the sphere lives:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-y220
Out[1]=1

Geometric dimension is the dimension of the shape itself:

In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-bx9tom
Out[2]=2

Membership testing:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-c7lq97
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-f70gib
Out[2]=2

Get conditions for point membership:

In[3]:=3
✖
https://wolfram.com/xid/0y7yz6-inebf9
Out[3]=3

Area:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-se0twe
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-e06l44
Out[2]=2

Centroid:

In[3]:=3
✖
https://wolfram.com/xid/0y7yz6-gwq4b4
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0y7yz6-oknxhk
Out[4]=4

Distance from a point:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-jcsb4b
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-8aexdg
Out[2]=2

The equidistance contours for a sphere:

In[3]:=3
✖
https://wolfram.com/xid/0y7yz6-ew8anh
Out[3]=3

Signed distance from a point:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-kjgbyj
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-zognbt
Out[2]=2

Nearest point in the region:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-d7g53y
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-mtue
Out[2]=2

Nearest points to an enclosing sphere:

In[3]:=3
✖
https://wolfram.com/xid/0y7yz6-e29k5d
In[4]:=4
✖
https://wolfram.com/xid/0y7yz6-5ksoo8
In[5]:=5
✖
https://wolfram.com/xid/0y7yz6-uv1cfm
Out[5]=5

A sphere is bounded:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-ypd96t
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-po0eks
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0y7yz6-dym4fu
In[4]:=4
✖
https://wolfram.com/xid/0y7yz6-i3tfrr
Out[4]=4

Find its range:

In[5]:=5
✖
https://wolfram.com/xid/0y7yz6-l3exhn
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0y7yz6-bx1r15
Out[6]=6

Integrate over a sphere region:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-fivgav
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-banwkr
Out[2]=2

Optimize over a sphere region:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-nf9ton
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-hyz4dq
Out[2]=2

Solve equations in a sphere region:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-bnrw6
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-lhnpf3
Out[2]=2

Applications  (5)Sample problems that can be solved with this function

Platonic polyhedra represented by spheres:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-bfsws8
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-efb6b4
Out[2]=2

Double helix:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-clnpvv
Out[1]=1

Bubbles:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-fp53yw
Out[1]=1

Use Sphere to render nodes in a GraphPlot3D:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-u52ea
Out[1]=1

Use Sphere in a BubbleChart3D:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-egr5c3
Out[1]=1

Properties & Relations  (8)Properties of the function, and connections to other functions

Use Scale to get ellipsoids:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-il7s6t
Out[1]=1

The 2D version of Sphere is Circle:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-biltrd
Out[1]=1

An implicit specification of a sphere generated by ContourPlot3D:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-be10oz
Out[1]=1

A parametric specification of a sphere generated by ParametricPlot3D:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-i7028d
Out[1]=1

ChemicalData plots a molecule using spheres and cylinders:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-e080hl
Out[1]=1

Several Import formats use spheres to represent molecules:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-iourzl
Out[1]=1

Circumsphere specifies a Sphere from points on the surface:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-7uiu1i
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-02w136
Out[2]=2

ImplicitRegion can represent any Sphere:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-hw5ae3
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-fw1b9n
Out[2]=2

Neat Examples  (4)Surprising or curious use cases

Random sphere collections:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-coltip
Out[1]=1

Cubic lattice of spheres:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-lq3
Out[1]=1

BCC lattice of spheres:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-xxl
Out[1]=1

Sample points used by NIntegrate:

In[1]:=1
✖
https://wolfram.com/xid/0y7yz6-n06bq
In[2]:=2
✖
https://wolfram.com/xid/0y7yz6-bankjl
Out[2]=2
Wolfram Research (2007), Sphere, Wolfram Language function, https://reference.wolfram.com/language/ref/Sphere.html (updated 2014).
✖
Wolfram Research (2007), Sphere, Wolfram Language function, https://reference.wolfram.com/language/ref/Sphere.html (updated 2014).

Text

Wolfram Research (2007), Sphere, Wolfram Language function, https://reference.wolfram.com/language/ref/Sphere.html (updated 2014).

✖
Wolfram Research (2007), Sphere, Wolfram Language function, https://reference.wolfram.com/language/ref/Sphere.html (updated 2014).

CMS

Wolfram Language. 2007. "Sphere." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Sphere.html.

✖
Wolfram Language. 2007. "Sphere." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Sphere.html.

APA

Wolfram Language. (2007). Sphere. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Sphere.html

✖
Wolfram Language. (2007). Sphere. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Sphere.html

BibTeX

@misc{reference.wolfram_2025_sphere, author="Wolfram Research", title="{Sphere}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Sphere.html}", note=[Accessed: 18-May-2025 ]}

✖
@misc{reference.wolfram_2025_sphere, author="Wolfram Research", title="{Sphere}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Sphere.html}", note=[Accessed: 18-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_sphere, organization={Wolfram Research}, title={Sphere}, year={2014}, url={https://reference.wolfram.com/language/ref/Sphere.html}, note=[Accessed: 18-May-2025 ]}

✖
@online{reference.wolfram_2025_sphere, organization={Wolfram Research}, title={Sphere}, year={2014}, url={https://reference.wolfram.com/language/ref/Sphere.html}, note=[Accessed: 18-May-2025 ]}