AsymptoticGreater[f,g,xx*]
xx*のときに ![]() または
または ![]() となる条件を与える.
となる条件を与える.
AsymptoticGreater[f,g,{x1,…,xn}{![]() ,…,
,…,![]() }]
}]
![]() のときに
のときに ![]() または
または ![]() となる条件を与える.
となる条件を与える.


AsymptoticGreater
AsymptoticGreater[f,g,xx*]
xx*のときに ![]() または
または ![]() となる条件を与える.
となる条件を与える.
AsymptoticGreater[f,g,{x1,…,xn}{![]() ,…,
,…,![]() }]
}]
![]() のときに
のときに ![]() または
または ![]() となる条件を与える.
となる条件を与える.
詳細とオプション


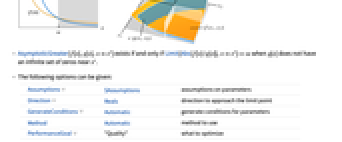

- 「漸近的により大きい」は,f は g のlittle-omegaである,f は g よりも程度が大きい,f は g よりも速く大きくなる,f は g を支配する等とも表現される.点 x*はコンテキストから推測されることが多い.
- 「漸近的により大きい」は順序関係で,
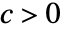 であるすべての定数について x が x*の近くにあるときに
であるすべての定数について x が x*の近くにあるときに![TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs] TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs]](Files/AsymptoticGreater.ja/9.png) であることを意味する.
であることを意味する. - 点の近くの関数や級数の単純で厳密な下限を表すために,また,方程式の解や複雑な計算の単純で厳密な下限を表すためにしばしば使われる.
- 有限極限点の x* および {
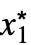 ,…,
,…,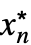 }については以下のようになる.
}については以下のようになる. -
AsymptoticGreater[f[x],g[x],xx*] すべての 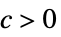 について,
について,![0<TemplateBox[{{x, -, {x, ^, *}}}, Abs]<delta(c,x^*) 0<TemplateBox[{{x, -, {x, ^, *}}}, Abs]<delta(c,x^*)](Files/AsymptoticGreater.ja/13.png) が
が![TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs] TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs]](Files/AsymptoticGreater.ja/14.png) を意味する
を意味する 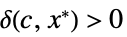 が存在する
が存在するAsymptoticGreater[f[x1,…,xn],g[x1,…,xn],{x1,…,xn}{ 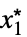 ,…,
,…,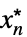 }]
}]すべての 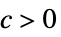 について,
について,![0<TemplateBox[{{{, {{{x, _, 1}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]<delta(epsilon,x^*) 0<TemplateBox[{{{, {{{x, _, 1}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]<delta(epsilon,x^*)](Files/AsymptoticGreater.ja/19.png) が
が![TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]>=c TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs] TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]>=c TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]](Files/AsymptoticGreater.ja/20.png) を意味する
を意味する 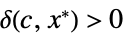 が存在する
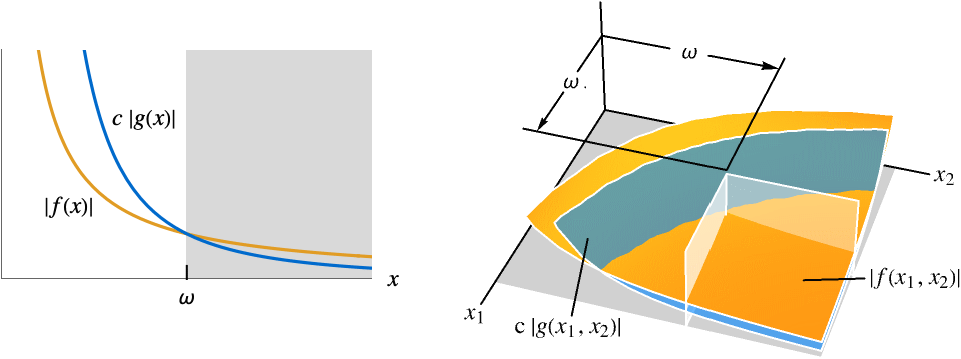
が存在する - 無限極限点については以下のようになる.
-
AsymptoticGreater[f[x],g[x],x∞] すべての 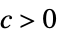 について,
について,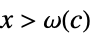 が
が![TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs] TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs]](Files/AsymptoticGreater.ja/25.png) を意味する
を意味する 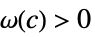 が存在する
が存在するAsymptoticGreater[f[x1,…,xn],g[x1,…,xn],{x1,…,xn}{∞,…,∞}] すべての 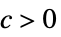 について,
について,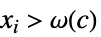 が
が![TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]>=c TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs] TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]>=c TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]](Files/AsymptoticGreater.ja/29.png) を意味する
を意味する 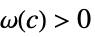 が存在する
が存在する - g[x]が x*付近で0の無限集合を持たない場合,AsymptoticGreater[f[x],g[x],xx*]はLimit[Abs[f[x]/g[x]],xx*]∞のときかつそのときに限り存在する.
- 次は,使用可能なオプションである.
-
Assumptions $Assumptions パラメータについての仮定 Direction Reals 極限点に近付く方向 GenerateConditions Automatic パラメータについての条件を生成する Method Automatic 使用するメソッド PerformanceGoal "Quality" 何を最適化するか - 次は,Directionの可能な設定である.
-
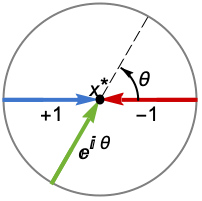
Reals または "TwoSided" 両実数方向から "FromAbove" または -1 上,つまりより大きい値から "FromBelow" または +1 下,つまりより小さい値から Complexes すべての複素方向から Exp[ θ] 方向 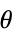 に
に{dir1,…,dirn} 変数 xiに方向 diriを使う - x*におけるDirectionExp[ θ]は,曲線の接線が極限点 x*に近付く方向を示す.
- 次は,GenerateConditionsの可能な設定である.
-
Automatic 一般的ではない条件のみ True すべての条件 False 条件なし None 条件が必要な場合には未評価で返す - PerformanceGoalの可能な設定には,$PerformanceGoal,"Quality","Speed"がある."Quality"設定のとき,AsymptoticGreaterはより多くの問題を解いたりより簡単な結果を与えたりすることが多いが,より多くの時間とメモリが必要になる可能性がある.
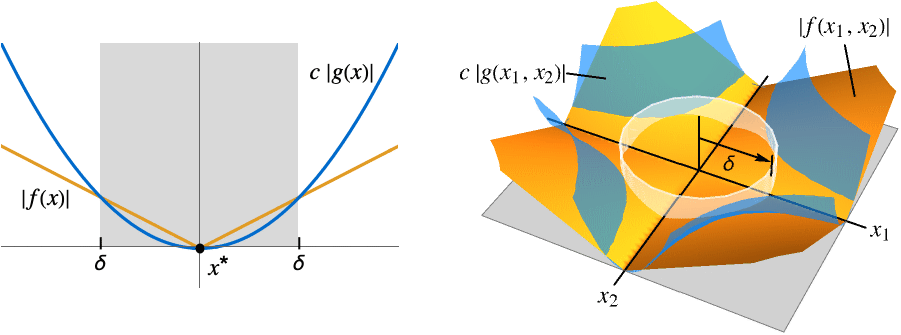
例題
すべて開く すべて閉じるスコープ (9)
オプション (10)
Assumptions (1)
Assumptionsを使ってパラメータについての条件を指定する:
Direction (5)
GenerateConditions (3)
デフォルトで,特殊な値でしか結果が無効にならない場合は,条件は生成されない:
GenerateConditions->Trueのときは,これらの一般的ではない条件も報告される:
PerformanceGoal (1)
PerformanceGoalを使って潜在的に高価な計算を回避する:
アプリケーション (18)
基本的なアプリケーション (4)
絶対誤差と相対誤差 (2)
漸近近似 (6)
![]() は関数であり,
は関数であり,![]() は
は ![]() の近くにおける
の近くにおける ![]() の近似であるとすると,
の近似であるとすると,![]() において
において ![]() ならこの近似は漸近的である.言い換えるなら,剰余すなわち誤差
ならこの近似は漸近的である.言い換えるなら,剰余すなわち誤差 ![]() は近似より漸近的に小さくなる.
は近似より漸近的に小さくなる.![]() が
が![]() における
における ![]() の漸近近似であることを示す:
の漸近近似であることを示す:
スターリングの公式![]() は
は ![]() のときの
のときの ![]() の漸近近似であることを示す:
の漸近近似であることを示す:
Seriesは初等関数と特殊関数の漸近近似を生成する.例えば,![]() における
における ![]() の次数-10の近似を生成する:
の次数-10の近似を生成する:
0におけるCot[x]の漸近級数を求める:
Gamma[x]の級数が-1において漸近的であることを示す:
近似される関数が近似点のすべての近傍で無限に何度も0に近付く場合は,漸近近似が微妙になるかもしれない.例として,![]() 近くにおける
近くにおける ![]() の漸近展開について考える:
の漸近展開について考える:
ベッセル関数のすべての零点において近似が完全に0にはならないので,この近似は漸近的ではない:
一方,決して0にならないハンケル関数 ![]() の近似について考える:
の近似について考える:
![]() なので,そのような近似2つの和であるこの近似はほぼ漸近的であると理解できる:
なので,そのような近似2つの和であるこの近似はほぼ漸近的であると理解できる:
AsymptoticIntegrateを使って定積分の漸近近似を生成する.例えば,![]() のときの
のときの![]() の漸近近似を求め,厳密値と比較する:
の漸近近似を求め,厳密値と比較する:
積分定数を考慮に入れる必要があるが,AsymptoticIntegrateを使って不定積分の漸近近似を生成する.![]() のときの
のときの![]() の近似について考える:
の近似について考える:
比較すべき記号結果はないが,過程が漸近的であると示すことはできる:
AsymptoticDSolveValueを使って微分方程式の漸近近似を生成する:
比較すべき厳密結果はないが,過程が漸近的であると示すことはできる:
NDSolveValueを使って得た数値解の値と比較する:
漸近尺度 (2)
計算の複雑性 (4)
単純なソートアルゴリズム(バブルソート,挿入ソート)は n 個のオブジェクトをソートするのに約 a n2ステップを要する.これに対し,最適化された一般的アルゴリズム(ヒープソート,マージソート)はソートを行うのに約 b n Log[n]のステップを要する.大量のオブジェクトに対しては,最適化されたアルゴリズムの方が常にソート時間が短くて済むことを示す:
ある種の特別なアルゴリズム(分布数え上げソート,基数ソート)は,考えられる入力についての情報が事前に分かっているので,c n 時間で実行することができる.使える場合には,これらの方が最適化アルゴリズムよりも速い:
バブルソートでは,隣接近傍が比較され,順序が狂っている場合には入れ替えられる.1回のパス(n-1 回の比較)の後で最大要素が末尾になる.その後このプロセスは,先頭の2つの要素のみが残るまで,残りの n-1個の要素に対して繰り返される.比較と入替えが c ステップだとすると,ソートのステップ総数は次のようになる:
マージソートでは,要素のリストが2つに分割され,それぞれの半分がソートされてから,その2つの半分が結合される.であるから,ソート時間T[n]は中間を計算する一定の時間 b,各半分をソートする時間2T[n/2],2つの半分を結合するための要素数の倍数 a n の合計になる:
再帰方程式を解いて n 個の要素をソートする時間 t を求める:
巡回セールスマン問題(TSP)は ![]() 個の都市を繋ぐ最短経路を求めるものである.馬鹿正直なアルゴリズムは
個の都市を繋ぐ最短経路を求めるものである.馬鹿正直なアルゴリズムは ![]() 通りの経路すべてを試そうとする.Held–Karpアルゴリズムは,それよりも効率よく約
通りの経路すべてを試そうとする.Held–Karpアルゴリズムは,それよりも効率よく約 ![]() ステップに短縮する.
ステップに短縮する.![]() であるからHeld–Karpアルゴリズムの方が速いことを示す:
であるからHeld–Karpアルゴリズムの方が速いことを示す:
どちらのアルゴリズムも巡回セールスマン問題の複雑性クラスは,時間![]() で解ける問題のEXPTIMEと同じくらいであることを示している.Held–Karpアルゴリズムは,
で解ける問題のEXPTIMEと同じくらいであることを示している.Held–Karpアルゴリズムは,![]() について
について ![]() を使うだけで十分である:
を使うだけで十分である:
解の近似は ![]() 回で求まるので,巡回セールスマン問題の近似は多項式時間で可解な問題の複雑性クラスPに属する.どの多項式アルゴリズムも指数アルゴリズムよりも速い.つまり
回で求まるので,巡回セールスマン問題の近似は多項式時間で可解な問題の複雑性クラスPに属する.どの多項式アルゴリズムも指数アルゴリズムよりも速い.つまり![]() である:
である:
特性と関係 (10)
AsymptoticGreaterは反射的ではない,つまり ![]() である:
である:
推移関係ではある.つまり,![]() かつ
かつ ![]() なら
なら ![]() ということを意味する:
ということを意味する:
Limit[Abs[f[x]/g[x]],xx0]∞のときかつそのときに限りAsymptoticGreater[f[x],g[x],xx0]である:
関連するガイド
-
▪
- 漸近解析
テキスト
Wolfram Research (2018), AsymptoticGreater, Wolfram言語関数, https://reference.wolfram.com/language/ref/AsymptoticGreater.html.
CMS
Wolfram Language. 2018. "AsymptoticGreater." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AsymptoticGreater.html.
APA
Wolfram Language. (2018). AsymptoticGreater. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AsymptoticGreater.html
BibTeX
@misc{reference.wolfram_2025_asymptoticgreater, author="Wolfram Research", title="{AsymptoticGreater}", year="2018", howpublished="\url{https://reference.wolfram.com/language/ref/AsymptoticGreater.html}", note=[Accessed: 16-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_asymptoticgreater, organization={Wolfram Research}, title={AsymptoticGreater}, year={2018}, url={https://reference.wolfram.com/language/ref/AsymptoticGreater.html}, note=[Accessed: 16-February-2026]}