Gamma

Gamma[z]

is the Euler gamma function TemplateBox[{z}, Gamma].

Gamma[a,z]

is the incomplete gamma function TemplateBox[{a, z}, Gamma2].

Gamma[a,z0,z1]

is the generalized incomplete gamma function TemplateBox[{a, {z, _, 0}}, Gamma2]-TemplateBox[{a, {z, _, 1}}, Gamma2].

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • The gamma function satisfies TemplateBox[{z}, Gamma]=int_0^inftyt^(z-1)e^(-t)dt.
  • The incomplete gamma function satisfies TemplateBox[{a, z}, Gamma2]=int_z^inftyt^(a-1)e^(-t)dt.
  • The generalized incomplete gamma function is given by the integral .
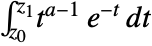  • Note that the arguments in the incomplete form of Gamma are arranged differently from those in the incomplete form of Beta.
  • Gamma[z] has no branch cut discontinuities.
  • Gamma[a,z] has a branch cut discontinuity in the complex z plane running from 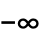to .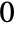
  • For certain special arguments, Gamma automatically evaluates to exact values.
  • Gamma can be evaluated to arbitrary numerical precision.
  • Gamma automatically threads over lists.
  • Gamma can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (8)

Integer values:

Half-integer values:

Evaluate numerically for complex arguments:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Series expansion at the origin:

Series expansion at Infinity:

Series expansion at a singular point:

Scope  (50)

Numerical Evaluation  (5)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Evaluate Gamma efficiently at high precision:

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

Compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix Gamma function using MatrixFunction:

Specific Values  (5)

Singular points of Gamma:

Values at infinity:

Find a local minimum as a root of (dTemplateBox[{x}, Gamma])/(d x)=0:

Evaluate the incomplete gamma function symbolically at integer and half‐integer orders:

Evaluate the generalized incomplete gamma function symbolically at half‐integer orders:

Visualization  (3)

Plot the Euler gamma function:

Plot the real part of TemplateBox[{z}, Gamma]:

Plot the imaginary part of TemplateBox[{z}, Gamma]:

Plot the incomplete gamma function for integer and half-integer orders:

Function Properties  (10)

Real domain of the complete Euler gamma function:

Complex domain:

Domain of the incomplete gamma functions:

The gamma function TemplateBox[{x}, Gamma] achieves all nonzero values on the reals:

The incomplete gamma function TemplateBox[{1, x}, Gamma2] achieves all positive real values for real inputs:

On the complexes, however, it achieves all nonzero values:

The incomplete gamma function TemplateBox[{{1, /, 2}, x}, Gamma2] has the restricted range :

The Euler gamma function has the mirror property TemplateBox[{TemplateBox[{z}, Conjugate, SyntaxForm -> SuperscriptBox]}, Gamma]=TemplateBox[{TemplateBox[{z}, Gamma]}, Conjugate]:

The complete gamma function TemplateBox[{x}, Gamma] is a meromorphic, nonanalytic function:

TemplateBox[{a, x}, Gamma2] is analytic in for positive integer :

But in general, it is neither an analytic nor a meromorphic function:

TemplateBox[{x}, Gamma] has both singularities and discontinuities on the non-positive integers:

TemplateBox[{x}, Gamma] is neither non-increasing nor non-decreasing:

TemplateBox[{a, x}, Gamma2] is a non-increasing function of when is a positive, odd integer:

But in general, it is neither non-increasing nor non-decreasing:

TemplateBox[{x}, Gamma] is not injective:

TemplateBox[{a, x}, Gamma2] is an injective function of for noninteger :

For integer , it may or may not be injective in :

TemplateBox[{x}, Gamma] is not surjective:

TemplateBox[{a, x}, Gamma2] is also not surjective:

Visualize for :

TemplateBox[{x}, Gamma] is neither non-negative nor non-positive:

TemplateBox[{a, x}, Gamma2] is non-negative for positive odd :

In general, it is neither non-negative nor non-positive:

TemplateBox[{x}, Gamma] is neither convex nor concave:

TemplateBox[{a, x}, Gamma2] is convex on its real domain for :

It is in general neither convex nor concave for other values of :

Differentiation  (4)

First derivative of the Euler gamma function:

First derivative of the incomplete gamma function:

Higher derivatives of the Euler gamma function:

Higher derivatives of the incomplete gamma function for an order :

Integration  (3)

Indefinite integral of the incomplete gamma function:

Indefinite integrals of a product involving the incomplete gamma function:

Numerical approximation of a definite integral int_1^2TemplateBox[{x}, Gamma]dx:

Series Expansions  (6)

Taylor expansion for the Euler gamma function around :

Plot the first three approximations for the Euler gamma function around :

Series expansion at infinity for the Euler gamma function (Stirling approximation):

Give the result for an arbitrary symbolic direction:

Series expansion for the incomplete gamma function at a generic point:

Series expansion for the incomplete gamma function at infinity:

Series expansion for the generalized incomplete gamma function at a generic point:

Gamma can be applied to a power series:

Integral Transforms  (4)

Compute the Laplace transform of the incomplete gamma function using LaplaceTransform:

InverseLaplaceTransform of the incomplete gamma function:

MellinTransform of the incomplete gamma function:

InverseMellinTransform of the Euler gamma function:

Function Identities and Simplifications  (5)

For positive integers (n-1)! = TemplateBox[{n}, Gamma]:

Use FullSimplify to simplify gamma functions:

The Euler gamma function basic relation, TemplateBox[{{z, +, 1}}, Gamma]=z TemplateBox[{z}, Gamma]:

The Euler gamma function of a double argument, TemplateBox[{{2, , x}}, Gamma]=(2^(2 x-1))/(sqrt(pi)) TemplateBox[{x}, Gamma] TemplateBox[{{x, +, {1, /, 2}}}, Gamma]:

Relation to the incomplete gamma function:

Function Representations  (5)

Integral representation of the Euler gamma function:

Integral representation of the incomplete gamma function:

The incomplete gamma function can be represented in terms of MeijerG:

The incomplete gamma function can be represented as a DifferentialRoot:

TraditionalForm formatting:

Generalizations & Extensions  (6)

Euler Gamma Function  (3)

Gamma threads element-wise over lists:

Series expansion at poles:

Expansion at symbolically specified negative integers:

TraditionalForm formatting:

Incomplete Gamma Function  (1)

Evaluate symbolically at integer and half‐integer orders:

Generalized Incomplete Gamma Function  (2)

Evaluate symbolically at integer and half‐integer orders:

Series expansion at a generic point:

Applications  (9)

Plot of the absolute value of Gamma in the complex plane:

Find the asymptotic expansion of ratios of gamma functions:

Volume of an ‐dimensional unit hypersphere:

Low‐dimensional cases:

Plot the volume of the unit hypersphere as a function of dimension:

Plot the real part of the incomplete gamma function over the parameter plane:

CDF of the ‐distribution:

Calculate the PDF:

Plot the CDF for different numbers of degrees of freedom:

Compute derivatives of the Gamma function with the BellY polynomial:

Compute as a limit of Gamma functions at Infinity:

Expectation value of the square root of a quadratic form over a normal distribution:

Compare with the closed-form result in terms of Gamma and CarlsonRG:

Represent Zeta in terms of Integrate and the Gamma function:

Properties & Relations  (7)

Use FullSimplify to simplify gamma functions:

Numerically find a root of a transcendental equation:

Sum expressions involving Gamma:

Generate from integrals, products, and limits:

Obtain Gamma as the solution of a differential equation:

Integrals:

Gamma can be represented as a DifferenceRoot:

Possible Issues  (2)

Large arguments can give results too large to be computed explicitly:

Machine‐number inputs can give high‐precision results:

Neat Examples  (3)

Nest Gamma over the complex plane:

Fractal from iterating Gamma:

Plot the Riemann surface of TemplateBox[{{1, /, 3}, z}, Gamma2]:

Wolfram Research (1988), Gamma, Wolfram Language function, https://reference.wolfram.com/language/ref/Gamma.html (updated 2022).

Text

Wolfram Research (1988), Gamma, Wolfram Language function, https://reference.wolfram.com/language/ref/Gamma.html (updated 2022).

CMS

Wolfram Language. 1988. "Gamma." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Gamma.html.

APA

Wolfram Language. (1988). Gamma. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Gamma.html

BibTeX

@misc{reference.wolfram_2025_gamma, author="Wolfram Research", title="{Gamma}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/Gamma.html}", note=[Accessed: 28-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_gamma, organization={Wolfram Research}, title={Gamma}, year={2022}, url={https://reference.wolfram.com/language/ref/Gamma.html}, note=[Accessed: 28-May-2025 ]}