BandstopFilter

BandstopFilter[data,{ω1,ω2}]

applies a bandstop filter with cutoff frequencies ω1 and ω2 to an array of data.

BandstopFilter[data,{{ω,q}}]

uses center frequency ω and quality factor q.

BandstopFilter[data,spec,n]

uses a filter kernel of length n.

BandstopFilter[data,spec,n,wfun]

applies a smoothing window wfun to the filter kernel.

Details and Options

  • Bandstop filtering is used in audio amplifiers, hearing aids and public address systems to attenuate mid-range frequencies in a signal while leaving the low and high frequencies unchanged.
  • BandstopFilter convolves a digital signal with a finite impulse response (FIR) kernel created using the window method.
  • Longer kernels result in a better frequency discrimination.
  • The data can be any of the following:
  • listarbitrary-rank numerical array
    tseriestemporal data such as TimeSeries and TemporalData
    imagearbitrary Image or Image3D object
    audioan Audio or Sound object
  • The range of frequencies that are attenuated is dependent on the values of the cutoff frequencies ω1 and ω2, with ω2>ω1.
  • When applied to images and multidimensional arrays, filtering is applied successively to each dimension starting at level 1. BandstopFilter[data,{{ω11,ω21},…}] uses the frequency {ω1i,ω2i} for the i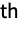^(th) dimension.
  • The frequency values ωi should be between 0 and .
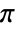  • BandstopFilter[data,{ω1,ω2}] uses a filter kernel length and smoothing window suitable for the cutoff frequencies {ω1,ω2} and the input data.
  • Typical smoothing windows wfun include:
  • BlackmanWindowsmoothing with a Blackman window
    DirichletWindowno smoothing
    HammingWindowsmoothing with a Hamming window
    {v1,v2,…}use a window with values vi
    fcreate a window by sampling f between 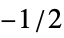and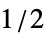
  • The following options can be given:
  • Padding "Fixed"the padding value to use
    SampleRate Automaticsample rate assumed for the input
  • By default, SampleRate->1 is assumed for images as well as data. For audio signals and time series, the sample rate is either extracted or computed from the input data.
  • With SampleRatesr, the cutoff frequency ωc should be between 0 and sr.

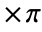Examples

open allclose all

Basic Examples  (3)

Bandstop filtering of a sum of cosines:

Compare with the ideal result, which is missing the middle frequency cosine:

Bandstop filtering of audio:

Bandstop filtering of an image:

Scope  (12)

Data  (7)

Filter a 1D pulse sequence:

Filter a 2D pulse sequence:

Filter a TimeSeries:

Bandstop filtering of a Sound object of a tri-tone signal:

Eliminate the middle tone using a bandstop filter with a Blackman window of length 101:

Bandstop filtering of a halftone image:

Bandstop filtering of a 3D image:

Filter using exact precision:

Parameters  (5)

A numeric cutoff frequency is interpreted as a quantity in units of radians per second:

Filter a white noise signal using a bandstop filter with cutoff frequencies of and :

Use center frequency of 8660 Hz and a factor of 1:

Make the quality factor smaller:

Use a filter of length 33:

Increase frequency discrimination by using a longer kernel:

Vary the amount of attenuation by using different window functions:

Vary the amount of attenuation by using the adjustable Kaiser window:

Use different center frequencies in each dimension:

Options  (3)

Padding  (1)

Different padding methods result in different edge effects:

SampleRate  (2)

Use a filter centered on the frequency π/2 assuming a sample rate of sr=1:

Assume a sample rate of sr=3:

Apply a bandstop filter to audio sampled at a rate of TemplateBox[{44100, "Hz", hertz, "Hertz"}, QuantityTF]:

Applications  (1)

On a modern 88-key piano, key 55 (note C5) has a fundamental frequency of approximately 523 Hz. Use BandstopFilter to effectively remove the first harmonic (1046 Hz) of this key while retaining the remaining frequencies in the following audio clip:

Use a narrow filter (Q=3) of length 101 centered on frequency 1046 Hz:

Compare the frequency spectra of the two audio clips:

Properties & Relations  (5)

Using cutoff frequencies of 0 and π returns a zero sequence:

Create a bandstop filter using LeastSquaresFilterKernel and a Hamming window:

Compare with the result of BandstopFilter:

Impulse response of a bandstop filter of length 21:

Magnitude spectrum of the filter:

Impulse response of a bandstop filter of length 21 without a smoothing window:

Magnitude spectrum of the filter:

The frequency discrimination of the bandstop filter improves as the length of the filter is increased:

Possible Issues  (1)

With PaddingNone, the output will be shorter than the input:

Wolfram Research (2012), BandstopFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/BandstopFilter.html (updated 2017).

Text

Wolfram Research (2012), BandstopFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/BandstopFilter.html (updated 2017).

CMS

Wolfram Language. 2012. "BandstopFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/BandstopFilter.html.

APA

Wolfram Language. (2012). BandstopFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BandstopFilter.html

BibTeX

@misc{reference.wolfram_2024_bandstopfilter, author="Wolfram Research", title="{BandstopFilter}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/BandstopFilter.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_bandstopfilter, organization={Wolfram Research}, title={BandstopFilter}, year={2017}, url={https://reference.wolfram.com/language/ref/BandstopFilter.html}, note=[Accessed: 22-December-2024 ]}