BaringhausHenzeTest

BaringhausHenzeTest[data]

Baringhaus–Henze検定を使い，データがMultinormalDistributionに従っているかどうかの検定を行う．

BaringhausHenzeTest[data,MultinormalDistribution[μ,Σ]]

データが，平均ベクトル μ，共分散行列 Σ で分布に従っているかどうかの検定を行う．

BaringhausHenzeTest[data,"property"]

"property"の値を返す．

詳細とオプション

  • BaringhausHenzeTestは，data がMultinormalDistributionから取られたという帰無仮説 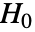とそうではないという対立仮説 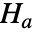で適合度検定を実行する．
  • BaringhausHenzeTestは，Baringhaus–Henze–Epps–Pulley多変量正規性検定，つまりBHEP検定としても知られている．
  • デフォルトで，確率値すなわち 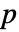値が返される．
  • 小さい 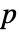値は data が多変量正規分布から来ている可能性が低いことを示す．
  • data は，一変量{x1,…,xn}あるいは多変量{{x1,y1,…},…,{xn,yn,…}}でよい．
  • Baringhaus–Henze検定は，事実上，無相関化された標準化 data と標準多変量ガウス特性関数Tβ=Expectation[n Abs[Ψemp[t]-Ψst[t]]2,{t1,…,td}]の間の距離 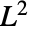に基づく経験特性関数検定統計 Tβを使う．ただし，=ProductDistribution[{NormalDistribution[0,β],d}]である． »
  • β 母数は正で，経験分布の平滑化を決定する．これは自動的に決定されるが，Method設定で変えることもできる．
  • BaringhausHenzeTest[data,MultinormalDistribution[μ,Σ],"HypothesisTestData"]はHypothesisTestDataオブジェクト htd を返す．これは，htd["property"]として追加的な検定結果および特性の抽出に使うことができる．
  • BaringhausHenzeTest[data,MultinormalDistribution[μ,Σ],"property"]を使って直接"property"の値を与えることができる．
  • 検定結果のレポートに関連する特性
  • "PValue" 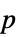値
    "PValueTable""PValue"のフォーマットされたバージョン
    "ShortTestConclusion"検定結果の簡単な説明
    "TestConclusion"検定結果の説明
    "TestData"検定統計と 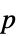値
    "TestDataTable""TestData"のフォーマットされたバージョン
    "TestStatistic"検定統計
    "TestStatisticTable"フォーマットされた"TestStatistic"
  • 次の特性はどの検定が行われているかに依存しない．
  • データ分布に関連する特性
  • "FittedDistribution"データのフィットした分布
    "FittedDistributionParameters"データの分布母数
  • 使用可能なオプション
  • Method Automatic 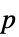値を計算するメソッド
    SignificanceLevel 0.05診断とレポートのための切捨て
  • 適合度検定では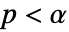， のときにのみ 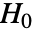が棄却されるような切捨て 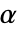が選択される．特性"TestConclusion"および"ShortTestConclusion"で使われる 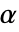の値はSignificanceLevelオプションで制御される．デフォルトで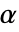， は0.05に設定されている． »
  • Method->"MonteCarlo"の設定では，入力 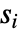と同じ長さのデータ集合が，フィットされた分布を使って 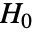のもとで生成される．次に，BaringhausHenzeTest[si,"TestStatistic"]からのEmpiricalDistributionを使って 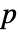値が推定される． »
  • Method{method,"SmoothingParameter"β}と設定すると，カスタムの平滑化母数 β を使うことができる．デフォルトは 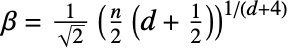である．この場合，検定はHenze-Zirkler検定としても知られるものになる． »

例題

すべて開くすべて閉じる

例  (3)

多変量正規性についての検定を行う：

Baringhaus–Henze検定から検定統計を抽出する：

フォーマットされた検定表を得る：

スコープ  (6)

検定  (3)

一変量の正規性についてBaringhaus–Henze検定を行う：

正規データの 値は，非正規データの 値と比べて大きい：

多変量の正規性についてBaringhaus–Henze検定を行う：

正規データの 値は，非正規データの 値と比べて大きい：

関連特性の抽出のためにHypothesisTestDataオブジェクトを作る：

抽出可能な特性：

レポート  (3)

Baringhaus–Henze検定の結果を表にする：

完全な検定表：

値の表：

検定統計：

カスタマイズされたレポート用にBaringhaus–Henze検定の表から項目を取り出す：

"ShortTestConclusion"と"TestConclusion"を使って検定の結論をレポートする：

有意水準が異なると，結論も異なることがある：

オプション  (3)

Method  (2)

Baringhaus–Henze検定に使われる平滑化母数 β を設定する：

平滑化母数 β は結果の 値に影響する：

モンテカルロ法に基づくメソッドで使われるランダムなシードを設定する：

シードは生成器の状態に影響を与え，結果の 値にもいくらか影響を与える：

モンテカルロ法と検定母数 β のカスタム設定を使って 値を求める：

デフォルトメソッドで得られた 値と比較する：

SignificanceLevel  (1)

"TestConclusion"と"ShortTestConclusion"で使う有意水準を設定する：

デフォルトで0.05が使われる：

アプリケーション  (4)

Baringhaus–Henze検定の検出力曲線（が偽であるときにこれを拒絶する確率）：

近似検出力曲線曲線を可視化する：

基礎となる分布がMultivariateTDistributionであり，検定サイズが0.05，サンプルサイズが43である場合の，Baringhaus–Henze検定の検出力を推定する：

連続時間ランダム過程がガウス過程であるかどうかを調べる．非整数ブラウン運動：

幾何ブラウン運動の対数の差：

コックス・インガソール・ロス(Cox–Ingersoll–Ross)過程の対数の差：

治療研究の前と後の患者の体重が記録されている．データが多変量正規分布に従っていれば，平均の多変量検定を使って対照群と実験群を識別することができる：

BaringhausHenzeTestを使って，データの3群が多変量正規分布に従っているかどうかを判定する：

Baringhaus–Henze検定はContおよびFTの群を棄却しなかった．TTestを使ってこの2群の平均が等しいかどうかを見る：

データが標準非相関二変量正規分布に従っているという仮説を検定する：

特性と関係  (5)

Baringhaus–Henze検定は，データに適用された線形変換が非特異であればアフィン不変である：

正規性についてのMardiaの結合検定はもまた，同じ特性を有する：

のもとでは，検定統計はLogNormalDistributionに漸近的に従う：

検定統計がLogNormalDistribution族からの分布に従うかどうかの検定を行う：

検定統計のヒストグラムを正規対数密度とともに示す：

BaringhausHenzeTest統計は，帰無仮説のもとでサンプルの経験特性関数と特性関数の間の距離に基づいている：

経験特性関数を定義し，距離を比較する：

BaringhausHenzeTestでレポートされた検定特性の値と比較する：

退化したサンプル共分散関数のサンプルについては，検定統計その最大値である4 n を与える：

対応する 値は0である：

小さい値の平滑化母数 β については，Baringhaus–Henze検定は裾部の動作により敏感である：

平滑化母数の関数としての多変量正規仮説の棄却率：

Mardia検定と比較する：

おもしろい例題  (1)

標準の正規境界で二変量分布を定義する：

境界分布は標準ガウス分布である：

二変量分布からのサンプル：

その成分のヒストグラムをプロットし，標準正規分布の密度関数と比較する：

分布 は同時ガウス分布ではない：

サンプルされた確率ベクトルを平面上に示す：

Wolfram Research (2015), BaringhausHenzeTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/BaringhausHenzeTest.html.

テキスト

Wolfram Research (2015), BaringhausHenzeTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/BaringhausHenzeTest.html.

CMS

Wolfram Language. 2015. "BaringhausHenzeTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BaringhausHenzeTest.html.

APA

Wolfram Language. (2015). BaringhausHenzeTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BaringhausHenzeTest.html

BibTeX

@misc{reference.wolfram_2024_baringhaushenzetest, author="Wolfram Research", title="{BaringhausHenzeTest}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/BaringhausHenzeTest.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_baringhaushenzetest, organization={Wolfram Research}, title={BaringhausHenzeTest}, year={2015}, url={https://reference.wolfram.com/language/ref/BaringhausHenzeTest.html}, note=[Accessed: 22-November-2024 ]}