WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

MultinormalDistribution
✖
MultinormalDistribution

✖

represents a multivariate normal distribution with zero mean and covariance matrix Σ.

✖

represents a multivariate normal (Gaussian) distribution with mean vector μ and covariance matrix Σ.

Details

  • The probability density for vector 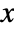in a multivariate normal distribution is proportional to .
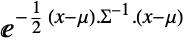  • MultinormalDistribution allows μ to be any vector of real numbers, and Σ any symmetric positive definite 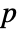× 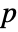matrix of real numbers with p=Length[μ].
  • The mean vector μ and covariance matrix Σ can be quantities such that μ⊗μ and Σ have the same unit dimensions componentwise. »
  • MultinormalDistribution can be used with such functions as Mean, CDF, and RandomVariate.

Background & Context

  • MultinormalDistribution[μ,Σ] represents a continuous multivariate statistical distribution supported over the set of 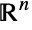of all 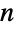-tuples 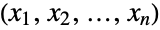and characterized by the property that each of the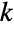 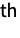^(th) (univariate) marginal distributions is a NormalDistribution for 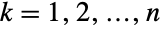. In other words, each of the variables 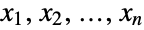satisfies xkNormalDistribution for 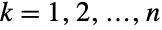. The multinormal distribution MultinormalDistribution[μ,Σ] is parametrized by a vector μ of real numbers and by a positive definite symmetric matrix Σ, which satisfy nLength[μ]Length[Σ] and which define the associated mean, variance, and covariance of the distribution. The multinormal distribution is sometimes referred to as the multivariate normal distribution, as a result of the fact that its univariate marginals are normally distributed.
  • The probability density function (PDF) of a multinormal distribution has a single absolute maximum, though like the binormal distribution (BinormalDistribution) it may have multiple "peaks" (i.e. relative maxima). In general, the tails of each of the associated marginal PDFs are "thin" in the sense that the marginal PDF decreases exponentially rather than algebraically for large values of 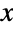. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of these marginal distributions.)
  • Most of the applications of the multinormal distribution correspond to the cases 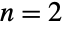(BinormalDistribution) or 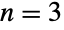rather than the general multinormal case. However, as a result of the multivariate central limit theorem, the multivariate normal distribution can be used to describe (at least qualitatively) any set of real-valued random variables, each of whose variates cluster around a given mean value. Even so, the bulk of the earliest literature (some of which dates back to the early 1800s) on multivariable extensions of the normal distribution focus on the bivariate and trivariate cases, which are applied in a wide range of fields, including genetics, materials science, evolutionary biology, economics, ecology, and medicine.
  • RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a multinormal distribution. Distributed[x,MultinormalDistribution[μ,Σ]] , written more concisely as xMultinormalDistribution[μ,Σ], can be used to assert that a random variable x is distributed according to a multinormal distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
  • The probability density and cumulative distribution functions for multinormal distributions may be given using PDF[MultinormalDistribution[μ,Σ],x] and CDF[MultinormalDistribution[μ,Σ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
  • DistributionFitTest can be used to test if a given dataset is consistent with a multinormal distribution, EstimatedDistribution to estimate a multinormal parametric distribution from given data, and FindDistributionParameters to fit data to a multinormal distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic multinormal distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic multinormal distribution.
  • TransformedDistribution can be used to represent a transformed multinormal distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a multinormal distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving multinormal distributions.
  • MultinormalDistribution is related to a number of other distributions, including the NormalDistribution and BinormalDistribution, as discussed above. The one-dimensional marginals of a MultinormalDistribution have a NormalDistribution, while each of the multivariate marginals is again an instance of MultinormalDistribution. MultinormalDistribution is a limiting case of MultivariateTDistribution in the sense that PDF[MultinormalDistribution[{μ1,μ2},{{1,ρ},{ ρ,1}}],{x,y}] is precisely the limit of PDF[MultivariateTDistribution[{μ1,μ2},{{1,ρ},{ ρ,1}},ν],{x,y}] as ν∞. Moreover, MultinormalDistribution can be obtained from LogMultinormalDistribution by a transformation (TransformedDistribution). MultinormalDistribution is also related to RiceDistribution and, because of its relation to the univariate NormalDistribution, is also related to LogNormalDistribution, DavisDistribution, LogLogisticDistribution, ExponentialDistribution, WeibullDistribution, GompertzMakehamDistribution, ExtremeValueDistribution, and GammaDistribution.

Examples

open allclose all

Basic Examples  (4)Summary of the most common use cases

Probability density function:

In[7]:=7
✖
https://wolfram.com/xid/0b7elrv0641id7p2-oy2ojl
Out[7]=7
In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-689i2
Out[3]=3

Cumulative distribution function:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-7a4qq4
Out[1]=1

Mean and variance:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-fnm69u
In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-zza0nn
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-1jvtw3
Out[3]=3

Covariance:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-sgrrls
In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-v9opdi
Out[2]=2

Scope  (8)Survey of the scope of standard use cases

Generate a sample of pseudorandom vectors from a bivariate normal distribution:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-ljmvtp

Visualize the sample using a histogram:

In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-okqqe1
Out[2]=2

Distribution parameters estimation:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-45b7g2

Estimate the distribution parameters from sample data:

In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-zwyjci
Out[2]=2

Goodness-of-fit test:

In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-k1bc33
Out[3]=3

Skewness and kurtosis are constant vectors:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-l46snq
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-14mzf9
Out[2]=2

Correlation:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-tsf0ki
In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-8yxe0v
In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-bxjlwn

The ImplicitRegion for 3D correlation coefficients of a multinormal distribution:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-uwfe5m
In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-lj6mc3
In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-cxciev

Use RandomPoint to sample from uniform distribution over 3D correlation coefficients region:

In[4]:=4
✖
https://wolfram.com/xid/0b7elrv0641id7p2-b7b6ro
In[5]:=5
✖
https://wolfram.com/xid/0b7elrv0641id7p2-dq3x
Out[5]=5

Estimate probability that determinant of the random correlation matrix is less than 0.1:

In[6]:=6
✖
https://wolfram.com/xid/0b7elrv0641id7p2-bkgrm2
Out[6]=6

Hazard function:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-y9qnwj
Out[1]=1

Univariate marginals follow a NormalDistribution:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-48ghft
In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-tnj6xf
Out[2]=2

Multivariate marginals follow a multivariate normal distribution:

In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-29y7hj
Out[3]=3

Consistent use of Quantity in parameters yields QuantityDistribution:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-ukzz1
Out[1]=1

Find standard deviations of each measurement:

In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-fxtz7g
Out[2]=2

Generalizations & Extensions  (1)Generalized and extended use cases

MultinormalDistribution[Σ] is understood to have zero mean:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-etepg
Out[1]=1

Applications  (2)Sample problems that can be solved with this function

Show a distribution function and its histogram in the same plot:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-ig1qzy

Compare the PDF to its histogram version:

In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-h0i29c
In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-ba9s1s
Out[3]=3

Compare the CDF to its histogram version:

In[4]:=4
✖
https://wolfram.com/xid/0b7elrv0641id7p2-5806k
Out[4]=4

Specify multinormal distribution for values of three incoming currents to a 4-way node:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-py26pm
Out[1]=1

Find the distribution of the current leaving the node:

In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-gdarv3
Out[2]=2

Find the 95% confidence interval for the current value:

In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-daqey
Out[3]=3

Properties & Relations  (10)Properties of the function, and connections to other functions

Equal probability contours for a bivariate normal distribution:

In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-o9k
Out[2]=2

The multinormal distribution is closed under affine transformation:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-uw25g7
In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-8t3p2g
In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-h7nhkv
Out[3]=3

For specific values:

In[4]:=4
✖
https://wolfram.com/xid/0b7elrv0641id7p2-172rna
In[5]:=5
✖
https://wolfram.com/xid/0b7elrv0641id7p2-32mxeg
Out[5]=5

Relationships to other distributions:

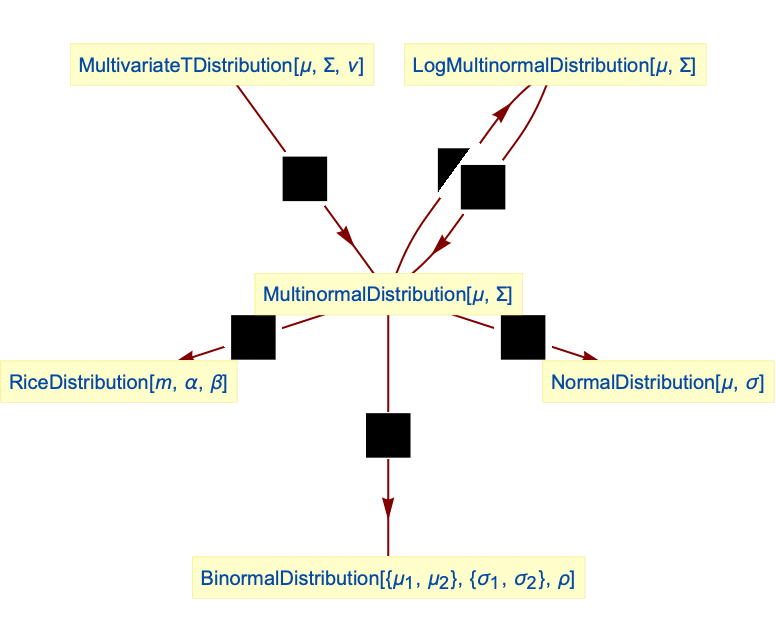
NormalDistribution is the univariate case of multinormal distribution:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-t7mes8
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-o74ppn
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-qdv2u2
Out[3]=3

BinormalDistribution is the two-dimensional case of multinormal distribution:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-l9jw29
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-qbcd3p
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-ssuls3
Out[3]=3

Multinormal distribution is the limit of MultivariateTDistribution as goes to :

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-pdcuvc
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-43l1h3
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-ztee3d
Out[3]=3

Multinormal distribution is related to RiceDistribution:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-0dy6kk
In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-60bpyx
Out[2]=2

LogMultinormalDistribution is a transformation of MultinormalDistribution:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-gov8at
In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-plabfy
Out[2]=2

NormalDistribution can be obtained from MultinormalDistribution:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-e76tlq
Out[1]=1

MultinormalDistribution is equivalent to CopulaDistribution with multinormal kernel and Gaussian marginals:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-pyufss

Corresponding multinormal distribution:

In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-gvyotj

The probability density functions are equal:

In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-hap7nq
Out[3]=3

Possible Issues  (2)Common pitfalls and unexpected behavior

MultinormalDistribution is not defined when μ is not a vector of real numbers:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-bu4jit
Out[1]=1

MultinormalDistribution is not defined when the dimensions of μ and Σ are not consistent:

In[2]:=2
✖
https://wolfram.com/xid/0b7elrv0641id7p2-dqrjwq
Out[2]=2

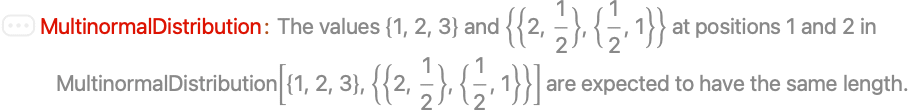
MultinormalDistribution is not defined when Σ is not symmetric and positive definite:

In[3]:=3
✖
https://wolfram.com/xid/0b7elrv0641id7p2-ef2
Out[3]=3

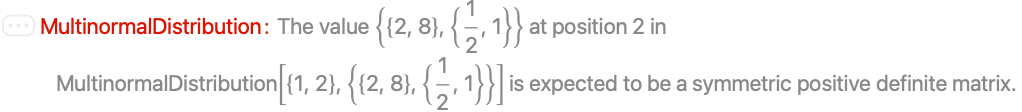
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:

In[1]:=1
✖
https://wolfram.com/xid/0b7elrv0641id7p2-cbt
Out[1]=1
Wolfram Research (2010), MultinormalDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MultinormalDistribution.html (updated 2016).
✖
Wolfram Research (2010), MultinormalDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MultinormalDistribution.html (updated 2016).

Text

Wolfram Research (2010), MultinormalDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MultinormalDistribution.html (updated 2016).

✖
Wolfram Research (2010), MultinormalDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MultinormalDistribution.html (updated 2016).

CMS

Wolfram Language. 2010. "MultinormalDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MultinormalDistribution.html.

✖
Wolfram Language. 2010. "MultinormalDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MultinormalDistribution.html.

APA

Wolfram Language. (2010). MultinormalDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MultinormalDistribution.html

✖
Wolfram Language. (2010). MultinormalDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MultinormalDistribution.html

BibTeX

@misc{reference.wolfram_2025_multinormaldistribution, author="Wolfram Research", title="{MultinormalDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MultinormalDistribution.html}", note=[Accessed: 08-July-2025 ]}

✖
@misc{reference.wolfram_2025_multinormaldistribution, author="Wolfram Research", title="{MultinormalDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MultinormalDistribution.html}", note=[Accessed: 08-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_multinormaldistribution, organization={Wolfram Research}, title={MultinormalDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/MultinormalDistribution.html}, note=[Accessed: 08-July-2025 ]}

✖
@online{reference.wolfram_2025_multinormaldistribution, organization={Wolfram Research}, title={MultinormalDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/MultinormalDistribution.html}, note=[Accessed: 08-July-2025 ]}