BaringhausHenzeTest

BaringhausHenzeTest[data]

用 Baringhaus–Henze 检验来检验数据是否遵循 MultinormalDistribution.

BaringhausHenzeTest[data,MultinormalDistribution[μ,Σ]]

检验数据是否遵循平均向量为 μ 、协方差矩阵为 Σ 的分布.

BaringhausHenzeTest[data,"property"]

返回 "property" 的值.

更多信息和选项

  • BaringhausHenzeTest 执行一个拟合优度检验, 零假设 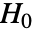下从 MultinormalDistribution 中提取 data ，而备择假设 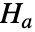下则不是.
  • BaringhausHenzeTest 也叫做 Baringhaus–Henze–Epps–Pulley 多变量正态性检验或者 BHEP 检验.
  • 默认情况下，一个概率值或 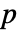-值被返回.
  • 一个小的 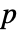-值意味着 data 不大可能来自一个多变量正态分布.
  • data 可以是单变量 {x1,…,xn} 或多变量 {{x1,y1,…},…,{xn,yn,…}}.
  • Baringhaus–Henze 检验实际上使用基于去相关标准化 data 的经验特征函数和标准的多变量高斯特征函数 Tβ=Expectation[n Abs[Ψemp[t]-Ψst[t]]2,{t1,…,td}] 之间的 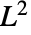距离的检验统计量 Tβ ，其中 =ProductDistribution[{NormalDistribution[0,β],d}]. »
  • 参数 β 为正且决定了经验分布的平滑性. 它是自动确定的，但是可以使用 Method 设置来更改.
  • BaringhausHenzeTest[data,MultinormalDistribution[μ,Σ],"HypothesisTestData"] 返回一个可以通过 htd["property"] 形式提取额外检验结果及属性的 HypothesisTestData 对象 htd .
  • BaringhausHenzeTest[data,MultinormalDistribution[μ,Σ],"property"] 可用于直接给出 "property" 的值.
  • 与报告检验结果相关的属性包括：
  • "PValue"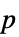-值
    "PValueTable""PValue" 的格式化形式
    "ShortTestConclusion"检验结果的简短说明
    "TestConclusion"检验结果的说明
    "TestData"检验统计量和 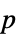-值
    "TestDataTable""TestData" 的格式化形式
    "TestStatistic"检验统计量
    "TestStatisticTable"格式化的"TestStatistic"
  • 下列属性与执行哪种检验无关.
  • 与数据分布相关的属性包括：
  • "FittedDistribution"数据的拟合分布
    "FittedDistributionParameters"数据的分布参数
  • 可以给出下列选项：
  • Method Automatic用于计算 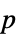-值的方法
    SignificanceLevel 0.05进行诊断并报告的临界值
  • 对于一个拟合优度检验，选择临界值 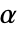使得只在 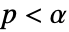的情况下拒绝 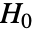. 用于 "TestConclusion" 和 "ShortTestConclusion" 属性的 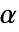值由 SignificanceLevel 选项来控制. 默认情况下 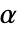被设为 0.05. »
  • 通过设置 Method->"MonteCarlo"，在 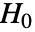下使用拟合分布生成一些长度相同的数据集作为输入 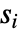. 然后用 BaringhausHenzeTest[si,"TestStatistic"] 中的 EmpiricalDistribution 来估计 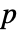-值. »
  • 设置 Method{method,"SmoothingParameter"β} 允许自定义平滑参数 β. 默认情况下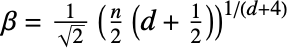，，这种情况下的检验亦被称作 Henze-Zirkler 检验. »

范例

打开所有单元关闭所有单元

基本范例  (3)

执行一个多变量正态性检验：

从 Baringhaus–Henze 检验中提取检验统计量：

获取格式化检验表：

范围  (6)

检验  (3)

执行一个单变量正态性 Baringhaus–Henze 检验：

正常数据的 -值相对于非正常数据的 -值是很大的：

执行一个多变量正态性 Baringhaus–Henze 检验：

正常数据的 -值相对于非正常数据的 -值是很大的：

为重复提取属性创建一个 HypothesisTestData 对象：

可供提取的属性：

报告  (3)

将 Baringhaus–Henze 检验结果制成表格：

完整的检验表格：

-值表：

检验统计量：

为定制报告从 Baringhaus–Henze 检验表中找出相应条目：

使用 "ShortTestConclusion" 和 "TestConclusion" 报告检验结论：

在不同的显著性水平上检验结论可能不同：

选项  (3)

Method  (2)

设置用于 Baringhaus–Henze 检验的平滑参数 β：

平滑参数 β 会影响相应的 -值：

设置用于基于蒙特卡罗方法的随机种子：

种子会影响生成器的状态，对相应的 -值也有一定的影响:

用蒙特卡洛方法和自定义检验参数 β 来找到 -值：

与用默认方法获得的 -值相比较：

SignificanceLevel  (1)

设置用于 "TestConclusion" 和 "ShortTestConclusion" 的显著性水平：

默认情况下使用 0.05 ：

应用  (4)

Baringhaus–Henze 检验的功效曲线（当 为假是将其拒绝的机率）：

显示近似的功效曲线：

当分布为MultivariateTDistribution、检验水平是 0.05 且样本量是43时估计 Baringhaus–Henze 检验的功效：

检查连续时间随机过程是否为高斯过程. 分数布朗运动：

几何布朗运动的对数的差分：

Cox–Ingersoll–Ross 过程的对数的差分：

病人在接受某种疗法前后的体重被记录下来. 如果数据遵循多变量正态分布，那么均值的多变量检验可用作区别对照组和实验组的检验：

用 BaringhausHenzeTest 确定这三组数据是否为多变量正态分布:

Cont 和 FT 组中的数据没有被 Baringhaus–Henze 检验拒绝. 使用 TTest 检验这两组的均值是否相同：

检验数据服从标准不相关双正态分布的假设：

属性和关系  (5)

如果应用于数据的线性变换是非奇异的，则 Baringhaus–Henze 检验是仿射不变的：

检验正态性的 Mardia 组合检验也享有一样的性质：

在 下检验统计量渐近地遵循 LogNormalDistribution：

查看检验统计量是否遵循 LogNormalDistribution 族中的某个分布：

显示具有对数正态密度的检验统计量的直方图：

BaringhausHenzeTest 统计量是基于样本经验特征函数和零假设下的特征函数之间的距离的：

定义经验特征函数并计算距离：

与 BaringhausHenzeTest 报告的检验统计量相比：

对具有退化样本协方差函数的样本, 检验统计量给出其最大值 4 n:

相应的 -值等于零：

当平滑参数 β 取较小的值时， Baringhaus–Henze 检验对尾的特性更敏感：

拒绝多变量正态性假设的比例是平滑参数的函数：

与 Mardia 检验对比：

巧妙范例  (1)

定义一个有标准正态边缘的双变量分布：

边缘分布是标准高斯分布：

双变量分布中的样本：

画出其分量的直方图并与标准正态分布的密度函数相比较：

分布不是联合高斯分布：

在平面上显示随机向量的抽样：

Wolfram Research (2015)，BaringhausHenzeTest，Wolfram 语言函数，https://reference.wolfram.com/language/ref/BaringhausHenzeTest.html.

文本

Wolfram Research (2015)，BaringhausHenzeTest，Wolfram 语言函数，https://reference.wolfram.com/language/ref/BaringhausHenzeTest.html.

CMS

Wolfram 语言. 2015. "BaringhausHenzeTest." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/BaringhausHenzeTest.html.

APA

Wolfram 语言. (2015). BaringhausHenzeTest. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BaringhausHenzeTest.html 年

BibTeX

@misc{reference.wolfram_2024_baringhaushenzetest, author="Wolfram Research", title="{BaringhausHenzeTest}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/BaringhausHenzeTest.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_baringhaushenzetest, organization={Wolfram Research}, title={BaringhausHenzeTest}, year={2015}, url={https://reference.wolfram.com/language/ref/BaringhausHenzeTest.html}, note=[Accessed: 22-November-2024 ]}