represents the Battle–Lemarié wavelet of order 3.
represents the Battle–Lemarié wavelet of order n evaluated on equally spaced interval {-10,10}.
BattleLemarieWavelet[n,lim]
represents the Battle–Lemarié wavelet of order n evaluated on equally spaced interval {-lim,lim}.


BattleLemarieWavelet
represents the Battle–Lemarié wavelet of order 3.
represents the Battle–Lemarié wavelet of order n evaluated on equally spaced interval {-10,10}.
BattleLemarieWavelet[n,lim]
represents the Battle–Lemarié wavelet of order n evaluated on equally spaced interval {-lim,lim}.
Details
- BattleLemarieWavelet defines a family of orthogonal wavelets based on orthonormalization of B-splines of degree n.
- BattleLemarieWavelet[n] is equivalent to BattleLemarieWavelet[n,10].
- The scaling function (
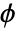 ) and wavelet function (
) and wavelet function (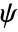 ) have infinite support with an exponential decay outside the interval -lim to lim. The functions are
) have infinite support with an exponential decay outside the interval -lim to lim. The functions are 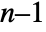 continuously differentiable.
continuously differentiable. - BattleLemarieWavelet can be used with such functions as DiscreteWaveletTransform, WaveletPhi, etc.
Examples
open all close allScope (9)
Basic Uses (4)
Wavelet Transforms (4)
Compute a DiscreteWaveletTransform:
View the tree of wavelet coefficients:
Get the dimensions of wavelet coefficients:
Plot the wavelet coefficients:
BattleLemarieWavelet can be used to perform a DiscreteWaveletPacketTransform:
View the tree of wavelet coefficients:
Get the dimensions of wavelet coefficients:
Plot the wavelet coefficients:
BattleLemarieWavelet can be used to perform a StationaryWaveletTransform:
View the tree of wavelet coefficients:
Get the dimensions of wavelet coefficients:
Plot the wavelet coefficients:
BattleLemarieWavelet can be used to perform a StationaryWaveletPacketTransform:
View the tree of wavelet coefficients:
Properties & Relations (11)
Lowpass filter coefficients approximately sum to unity; ![]() :
:
Highpass filter coefficients approximately sum to zero; ![]() :
:
Scaling function integrates to unity; ![]() :
:
Wavelet function integrates to zero; ![]() :
:
For even order n, scaling function is symmetrical about 1/2:
For even order n, wavelet function is antisymmetrical about 1/2:
For odd order n, scaling function is symmetrical about 0:
For odd order n, wavelet function is symmetrical about 1/2:
![]() satisfies the recursion equation
satisfies the recursion equation ![]() :
:
Plot the components and the sum of the recursion:
![]() satisfies the recursion equation
satisfies the recursion equation ![]() :
:
Plot the components and the sum of the recursion:
Frequency response for ![]() is given by
is given by ![]() :
:
The filter is a lowpass filter:
Frequency response for ![]() is given by
is given by ![]() :
:
The filter is a highpass filter:
Possible Issues (1)
BattleLemarieWavelet is restricted to n less than 15:
BattleLemarieWavelet is not defined when n is not a positive machine integer:
Tech Notes
Related Guides
History
Text
Wolfram Research (2010), BattleLemarieWavelet, Wolfram Language function, https://reference.wolfram.com/language/ref/BattleLemarieWavelet.html.
CMS
Wolfram Language. 2010. "BattleLemarieWavelet." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BattleLemarieWavelet.html.
APA
Wolfram Language. (2010). BattleLemarieWavelet. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BattleLemarieWavelet.html
BibTeX
@misc{reference.wolfram_2025_battlelemariewavelet, author="Wolfram Research", title="{BattleLemarieWavelet}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/BattleLemarieWavelet.html}", note=[Accessed: 27-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_battlelemariewavelet, organization={Wolfram Research}, title={BattleLemarieWavelet}, year={2010}, url={https://reference.wolfram.com/language/ref/BattleLemarieWavelet.html}, note=[Accessed: 27-February-2026]}