BesselJZero

✖
`BesselJZero`

✖

BesselJZero[n,k]

代表贝塞尔函数的第 k 个零点.

✖

BesselJZero[n,k,x₀]

代表大于 x₀ 的第 k 个零点.

更多信息

数学函数，适用于符号和数值运算.
只要指定的零点存在，N[BesselJZero[n,k]] 就给出一个数值近似值.
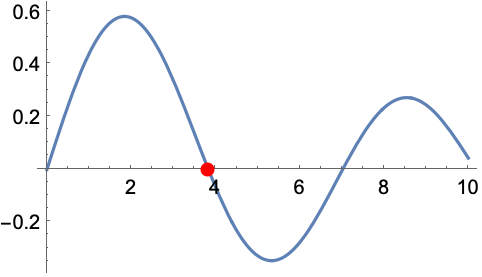
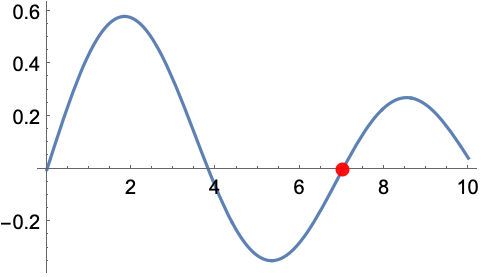
BesselJZero[n,k] 代表大于0的第 k 个零点.
BesselJZero 可以计算至任意数值精度.
BesselJZero 自动线性作用于列表. »

范例

打开所有单元关闭所有单元

基本范例 (5)常见实例总结

数值计算：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-mng3w

Out[1]=1

符号计算：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-clelng

Out[1]=1

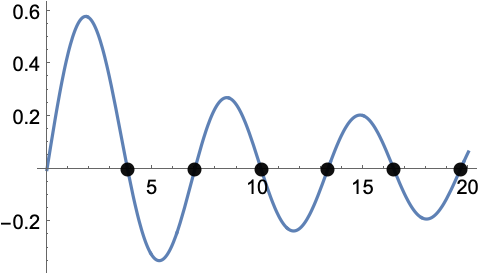
在实数子集上显示 BesselJ 函数的零点：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-b44iq5

Out[1]=1

在原点的级数展开：

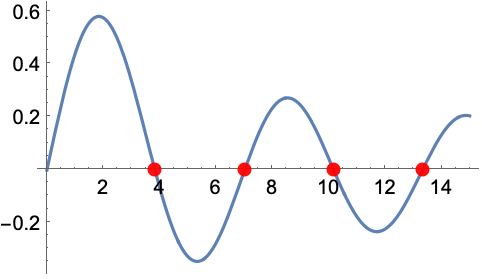
In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-qhqqh

Out[1]=1

TraditionalForm 格式：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-fm3bjb

范围 (19)标准用法实例范围调查

数值计算 (8)

数值化计算：

In[3]:=3

✖

https://wolfram.com/xid/0mlgadgcsomw-l274ju

Out[3]=3

求大于 40 的第一个零点：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-gvjp4u

Out[1]=1

高精度计算：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-b0wt9

Out[1]=1

高精度的高效计算：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-di5gcr

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0mlgadgcsomw-bq2c6r

Out[2]=2

第二个参数为非整数的情况下进行计算：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-oy0vsi

Out[1]=1

对于 BesselJZero[ν,k-α/π]，结果为的零点：

In[2]:=2

✖

https://wolfram.com/xid/0mlgadgcsomw-lbqfty

Out[2]=2

或用 Around 计算一般情况下的统计区间：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-c1pfqn

Out[1]=1

BesselJZero 逐个作用于列表的每个元素：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-e78ss3

Out[1]=1

自动逐项计算数组中每个元素的值：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-ojxade

Out[1]=1

或用 MatrixFunction 计算矩阵形式的 BesselJZero 函数：

In[2]:=2

✖

https://wolfram.com/xid/0mlgadgcsomw-blv2yt

Out[2]=2

特殊值 (3)

无穷处的极限值：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-ciezym

Out[1]=1

前三个零点：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-e3n9bq

Out[1]=1

使用 Solve 找到 BesselJ[1,x] 的第一个零点：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-f2hrld

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0mlgadgcsomw-bk6w11

Out[2]=2

可视化 (3)

将 BesselJ 的零点可视化为阶跃函数：

In[19]:=19

✖

https://wolfram.com/xid/0mlgadgcsomw-g7ixf5

Out[19]=19

显示 BesselJ 函数的零点：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-ecj8m7

Out[1]=1

显示大于 6 的第一个零点：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-df2nos

Out[1]=1

微分和级数展开式 (5)

求 Bessel zero 关于 k 的导数：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-saqgpp

Out[1]=1

二阶导：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-nfbe0l

Out[1]=1

使用 Series 求泰勒展开：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-ewr1h8

Out[1]=1

求在 Infinity 处的级数展开：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-syq

Out[1]=1

普通点的泰勒展开：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-jwxla7

Out[1]=1

应用 (3)用该函数可以解决的问题范例

求出带有狄利克雷边界条件圆鼓的前十个本征模：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-jjf5xo

Out[1]=1

构造一个由一定混合模构成的振幅：

In[2]:=2

✖

https://wolfram.com/xid/0mlgadgcsomw-c8ko17

圆形密度图：

In[3]:=3

✖

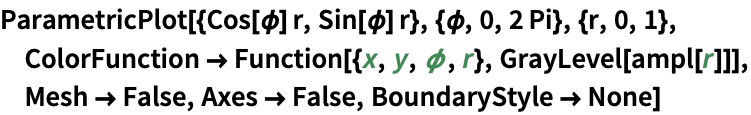
https://wolfram.com/xid/0mlgadgcsomw-cfo6eq

Out[3]=3

半径鼓位移剖面：

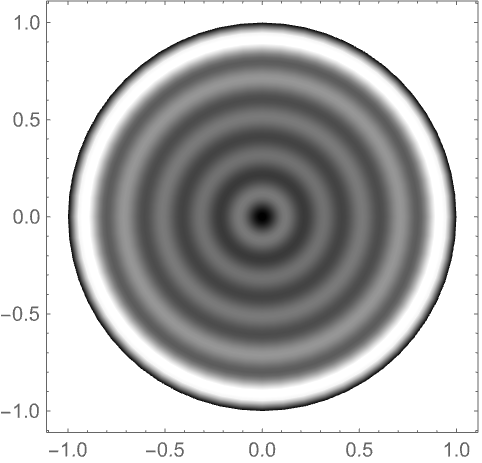
In[4]:=4

✖

https://wolfram.com/xid/0mlgadgcsomw-6w1r1

Out[4]=4

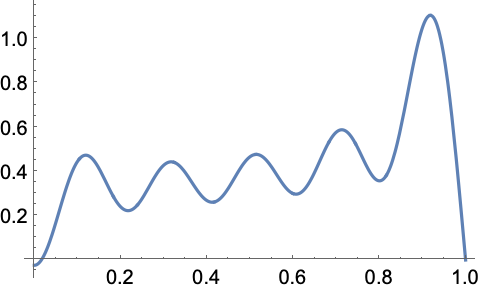
找出 Rayleigh criterion 中的系数用于衍射限光装置：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-gfbw2h

Out[1]=1

分析计 Disk 上直角坐标中 Laplacian 的特征值：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-ukyzsi

Out[1]=1

属性和关系 (1)函数的属性及与其他函数的关联

k 较大时的 BesselJZero[ν,k] 渐近状态：

In[1]:=1

✖

https://wolfram.com/xid/0mlgadgcsomw-bgfojp

Out[1]=1

顶部