BlockDiagonalMatrix[{d1,d2,…}]
対角ブロック diを持つブロック対角行列を構造化配列として表す.
BlockDiagonalMatrix[mat]
ブロック対角行列 mat を構造化配列に変換する.


BlockDiagonalMatrix
BlockDiagonalMatrix[{d1,d2,…}]
対角ブロック diを持つブロック対角行列を構造化配列として表す.
BlockDiagonalMatrix[mat]
ブロック対角行列 mat を構造化配列に変換する.
詳細とオプション


- ブロック対角行列は,構造化配列として表されているときは,Det,Inverse,LinearSolveを含む関数におけるより効率的な保存と操作を可能にする.
- ブロック対角行列は,偏微分方程式の離散化で使用されるように,複数の接続された成分を持つグラフの隣接行列,対角行列を持つ完全な行列のテンソル積(クロネッカー積),ジョルダン分解およびコア零分解の出力として自然に発生する.
- ブロック対角行列は対角行列を一般化する.ここで,対角要素はそれ自体が行列である.
- 対角ブロック diは正方行列でなければならない.
- ブロック対角行列の逆行列もまたブロック対角行列である.
- ブロック対角行列の行列式は対角ブロックの行列式の積である.
- BlockDiagonalMatrix sa については以下の特性"prop" に sa["prop"]でアクセスできる.
-
"Blocks" 対角ブロックのリスト "RowPermutation" 置換リストとして表された行の置換 "ColumnPermutation" 置換リストとして表された列の置換 "Properties" サポートされる特性のリスト "Structure" 構造化配列の型 "StructuredData" 構造化配列によって保存された内部データ "StructuredAlgorithms" 構造化配列についての特別なメソッドがある関数のリスト "Summary" Datasetとして表されたまとめの情報 - Normal[BlockDiagonalMatrix[…]]はブロック対角行列を通常の行列として与える.
- BlockDiagonalMatrix[…,TargetStructure->struct]は,struct で指定された形式でブロック対角行列を返す.次は,使用可能な設定である.
-
Automatic 返す表現を自動選択する "Dense" 行列を密な行列として表す "Sparse" 行列を疎な配列として返す "Structured" 行列を構造化配列として返す - BlockDiagonalMatrix[…,TargetStructureAutomatic]はBlockDiagonalMatrix[…,TargetStructure"Structured"]に等しい.
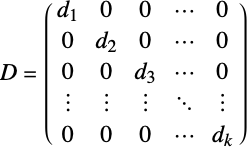
例題
すべて開く すべて閉じる例 (1)
スコープ (6)
BlockDiagonalMatrixオブジェクトは行列に関する情報を与える特性を含む:
"RowPermutation"特性はもとの行列に施された行置換を符号化する:
"ColumnPermutation"特性はもとの行列に施された列置換を符号化する:
"Summary"特性は配列についての情報の簡単なまとめを与える:
"StructuredAlgorithms"特性は表現の構造を使う関数のリストを与える:
構造化アルゴリズムは,適切な場合は別のBlockDiagonalMatrixオブジェクトを返す:
bd にその転置を掛けると別のブロック対角行列が与えられる:
BlockDiagonalMatrixの要素は強制的にブロックの非零要素の精度になる:
SparseArrayからブロック対角行列を構築する:
アプリケーション (5)
対角行列と正方行列のクロネッカー(Kronecker)積はブロック対角行列である:
非連結グラフは,ブロック対角行列として表すことができる隣接行列を持つ:
これはConnectedGraphComponentsを使うことに等しい:
高速フーリエ変換(FFT)の効率は2つの小さいフーリエ行列から大きいフーリエ行列が形成できる点にかかっている.大きさが p と q の2つの小さいフーリエ行列を生成する:
大きさが p q のフーリエ行列は,より単純な4つの行列の積として表すことができる:
結果の行列がFourierMatrixの結果と等しいことを示す:
ベクトルの離散フーリエ変換はフーリエ行列の因子を連続的にベクトルに掛けることで計算できる:
結果はFourierをベクトルに適用したものと等しい:
特性と関係 (4)
SparseArray[BlockDiagonalMatrix[…]]を使ってSparseArrayとしての表現を得る:
対角行列は1×1ブロックを持つブロック対角行列として扱われる:
BlockDiagonalMatrixブロックを持つBlockDiagonalMatrixオブジェクトは単一のBlockDiagonalMatrixオブジェクトに平坦化される:
BlockDiagonalMatrixは,与えられた行列が対角ブロックに分割できない場合,あるいは対角ブロックの形式に変換できない場合は行列そのものを返す:
関連するガイド
-
▪
- 構造化配列
テキスト
Wolfram Research (2022), BlockDiagonalMatrix, Wolfram言語関数, https://reference.wolfram.com/language/ref/BlockDiagonalMatrix.html (2023年に更新).
CMS
Wolfram Language. 2022. "BlockDiagonalMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/BlockDiagonalMatrix.html.
APA
Wolfram Language. (2022). BlockDiagonalMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BlockDiagonalMatrix.html
BibTeX
@misc{reference.wolfram_2025_blockdiagonalmatrix, author="Wolfram Research", title="{BlockDiagonalMatrix}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/BlockDiagonalMatrix.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_blockdiagonalmatrix, organization={Wolfram Research}, title={BlockDiagonalMatrix}, year={2023}, url={https://reference.wolfram.com/language/ref/BlockDiagonalMatrix.html}, note=[Accessed: 05-February-2026]}