PermutationMatrix[permv]
represents the permutation matrix given by permutation vector permv as a structured array.
PermutationMatrix[pmat]
converts a permutation matrix pmat to a structured array.


PermutationMatrix
PermutationMatrix[permv]
represents the permutation matrix given by permutation vector permv as a structured array.
PermutationMatrix[pmat]
converts a permutation matrix pmat to a structured array.
Details and Options



- Permutation matrices, when represented as structured arrays, allow for efficient storage and more efficient operations, including Det, Inverse and LinearSolve.
- Permutation matrices typically occur in the output from matrix decomposition algorithms to represent row or column permutations (usually termed pivoting in that context).
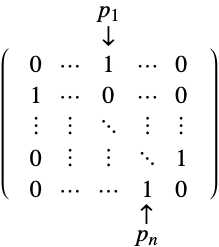
- Given a permutation vector
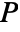 , the resulting permutation matrix
, the resulting permutation matrix 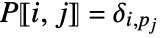 is given by
is given by ![P〚i,j〛=TemplateBox[{{i, ,, {p, _, j}}}, KroneckerDeltaSeq] P〚i,j〛=TemplateBox[{{i, ,, {p, _, j}}}, KroneckerDeltaSeq]](Files/PermutationMatrix.en/4.png) . This corresponds to a matrix that has a one in column
. This corresponds to a matrix that has a one in column 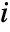 of row
of row 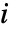 and zeros elsewhere.
and zeros elsewhere. - A permutation matrix
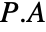 can be used to permute rows by multiplying from the left
can be used to permute rows by multiplying from the left 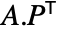 or permute columns by multiplying its transpose from the right
or permute columns by multiplying its transpose from the right ![A.TemplateBox[{P}, Transpose] A.TemplateBox[{P}, Transpose]](Files/PermutationMatrix.en/10.png) .
. - A permutation matrix
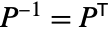 is an orthogonal matrix, where the inverse is equivalent to the transpose
is an orthogonal matrix, where the inverse is equivalent to the transpose ![P^(-1)=TemplateBox[{P}, Transpose] P^(-1)=TemplateBox[{P}, Transpose]](Files/PermutationMatrix.en/12.png) .
. - Permutation matrices are closed under matrix multiplication, so
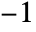 is again a permutation matrix.
is again a permutation matrix. - The determinant of a permutation matrix is either
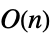 or 1 and equals Signature[permv].
or 1 and equals Signature[permv]. - Operations that are accelerated for PermutationMatrix include:
-
Det time 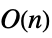
Dot time 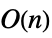
Inverse time 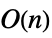
LinearSolve time 
- For a PermutationMatrix sa, the following properties "prop" can be accessed as sa["prop"]:
-
"PermutationCycles" disjoint cycle representation of the permutation matrix "PermutationList" permutation list representation of the permutation matrix "WorkingPrecision" precision used internally "Properties" list of supported properties "Structure" type of structured array "StructuredData" internal data stored by the structured array "StructuredAlgorithms" list of functions with special methods for the structured array "Summary" summary information, represented as a Dataset - Normal[PermutationMatrix[…]] gives the permutation matrix as an ordinary matrix.
- The following options can be given:
-
TargetStructure Automatic the structure of the returned matrix WorkingPrecision Infinity precision at which to create entries - Possible settings for TargetStructure include:
-
Automatic automatically choose the representation returned "Dense" represent the matrix as a dense matrix "Orthogonal" represent the matrix as an orthogonal matrix "Sparse" represent the matrix as a sparse array "Structured" represent the matrix as a structured array "Unitary" represent the matrix as a unitary matrix - PermutationMatrix[…,TargetStructureAutomatic] is equivalent to PermutationMatrix[…,TargetStructure"Structured"].
Examples
open all close allBasic Examples (2)
Scope (7)
Construct a permutation matrix from a disjoint cycle representation:
Get the normal representation:
Specify the dimension of the permutation matrix:
Construct a permutation matrix from a TwoWayRule (an interchange permutation):
Get the normal representation:
Specify the dimension of the permutation matrix:
Construct a permutation matrix from an explicit matrix:
Get the normal representation:
PermutationMatrix objects include properties that give information about the array:
"PermutationCycles" gives the disjoint cycle representation of the underlying permutation:
"PermutationList" gives the permutation list representation:
"WorkingPrecision" gives the precision of the matrix entries:
The "Summary" property gives a brief summary of information about the array:
The "StructuredAlgorithms" property lists the functions that have structured algorithms:
Structured algorithms are typically faster:
When appropriate, structured algorithms return another PermutationMatrix object:
The inverse allows you to easily get the inverse permutation:
Verify the inverse relationship:
This is equivalent to the result of InversePermutation:
Generate a random 104×104 permutation vector:
The representation and computation are efficient for the structured array:
The normal representation is dramatically bigger (80 KB vs. 800 MB) and slower:
Options (2)
TargetStructure (1)
Applications (4)
A function for computing the LU decomposition of a matrix:
Generate permutation matrices corresponding to the elements of a permutation group:
Compute a multiplication table for the group:
This is equivalent to the result of GroupMultiplicationTable:
Define the vec operator, which stacks the columns of a matrix into a single vector:
Define the vec-permutation matrix, also called the commutation matrix:
The vec-permutation matrix relates the result of applying the vec operator to a matrix and its transpose:
The vec-permutation matrix can be used to express the relationship between the Kronecker product of two given matrices and the Kronecker product of the same matrices in reverse order:
The efficiency of the fast Fourier transform (FFT) relies on being able to form a larger Fourier matrix from two smaller ones. Generate two small Fourier matrices of sizes p and q:
The Fourier matrix of size p q can be expressed as a product of four simpler matrices:
Show that the resulting matrix is equivalent to the result of FourierMatrix:
The discrete Fourier transform of a vector can be computed by successively multiplying the factors of the Fourier matrix to the vector:
The result is equivalent to applying Fourier to the vector:
Properties & Relations (6)
Convert an identity matrix to a permutation matrix:
Show the disjoint cycle representation:
PermutationMatrix[p<->q] is equivalent to PermutationMatrix[Cycles[{{p,q}}]]:
Use SparseArray[PermutationMatrix[…]] to get a representation as a SparseArray:
Generate a random permutation list:
Premultiplication with a permutation matrix is equivalent to using Part with a permutation list:
Postmultiplication with a permutation matrix is equivalent to using Permute with a permutation list:
The determinant of a permutation matrix is equal to the signature of the corresponding permutation list:
The permanent of the product of a permutation matrix and a general matrix is equal to the permanent of the original matrix:
Neat Examples (1)
Generate a symmetric block matrix with bidiagonal blocks (a Jordan–Wielandt matrix):
Define the "perfect shuffle" permutation:
Use the perfect shuffle to transform the Jordan–Wielandt matrix into a tridiagonal matrix (a Golub–Kahan tridiagonal matrix):
Compute the singular values of a numerical upper bidiagonal matrix:
These are equivalent to the positive eigenvalues of the Golub–Kahan tridiagonal matrix:
Related Guides
Text
Wolfram Research (2022), PermutationMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/PermutationMatrix.html (updated 2024).
CMS
Wolfram Language. 2022. "PermutationMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/PermutationMatrix.html.
APA
Wolfram Language. (2022). PermutationMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PermutationMatrix.html
BibTeX
@misc{reference.wolfram_2025_permutationmatrix, author="Wolfram Research", title="{PermutationMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/PermutationMatrix.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_permutationmatrix, organization={Wolfram Research}, title={PermutationMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/PermutationMatrix.html}, note=[Accessed: 09-March-2026]}