CDFWavelet

CDFWavelet[]

タイプ"9/7"のCohen–Daubechies–Feauveauウェーブレットを表す．

CDFWavelet["type"]

タイプ"type"のCohen–Daubechies–Feauveauウェーブレットを表す．

詳細

  • CDFWaveletは双直交ウェーブレット群を定義する．
  • 使用可能な"type"の形
  • "5/3"JPEG2000の可逆圧縮で使われる
    "9/7"JPEG2000の非可逆圧縮で使われる
  • スケーリング関数(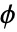)とウェーブレット関数(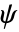)はコンパクトサポートを持つ．両関数は対称である．
  • CDFWaveletはDiscreteWaveletTransform，WaveletPhi等の関数で使うことができる．

例題

すべて開くすべて閉じる

例  (3)

スケーリング関数：

ウェーブレット関数：

フィルタ係数：

スコープ  (16)

基本的な用法  (10)

主ローパスフィルタ係数を計算する：

双対ローパスフィルタ係数：

主ハイパスフィルタ係数：

双対ハイパスフィルタ係数：

リフティングフィルタ係数：

関数を生成してリフティングウェーブレット変換を計算する：

主スケーリング関数：

双対スケーリング関数：

異なる再帰レベルを使ってスケーリング関数をプロットする：

主ウェーブレット関数：

双対ウェーブレット関数：

異なる再帰レベルを使ってウェーブレット関数をプロットする：

ウェーブレット変換  (5)

DiscreteWaveletTransformを計算する：

ウェーブレット係数の木を見る：

ウェーブレット係数の次元を得る：

ウェーブレット係数をプロットする：

DiscreteWaveletPacketTransformを計算する：

ウェーブレット係数の木を見る：

ウェーブレット係数の次元を得る：

ウェーブレット係数をプロットする：

StationaryWaveletTransformを計算する：

ウェーブレット係数の木を見る：

ウェーブレット係数の次元を得る：

ウェーブレット係数をプロットする：

StationaryWaveletPacketTransformを計算する：

ウェーブレット係数の木を見る：

ウェーブレット係数の次元を得る：

ウェーブレット係数をプロットする：

LiftingWaveletTransformを計算する：

ウェーブレット係数の木を見る：

ウェーブレット係数の次元を得る：

ウェーブレット係数をプロットする：

より高い次元  (1)

多変量スケーリング関数と多変量ウェーブレット関数はそれぞれの一変量関数の積である：

特性と関係  (16)

ローパスフィルタ係数の総和は単位元である．：

ハイパスフィルタ係数の総和は0である．：

双対ローパスフィルタ係数の総和は単位元である．：

双対ハイパスフィルタ係数の総和は0である．：

スケーリング関数を積分すると単位元になる．：

双対スケーリング関数を積分すると単位元になる．：

ウェーブレット関数を積分すると0になる．：

双対ウェーブレット関数を積分すると0になる．：

は再帰方程式 を満足する：

構成要素と再帰の総和をプロットする：

は再帰方程式 を満足する：

構成要素と再帰の総和をプロットする：

は再帰方程式 を満足する：

構成要素と再帰の総和をプロットする：

は再帰方程式 を満足する：

構成要素と再帰の総和をプロットする：

に対する周波数応答は で与えられる：

フィルタはローパスフィルタである：

Fのフーリエ(Fourier)変換は で与えられる：

に対する周波数応答はで与えられる：

フィルタは双対ローパスフィルタである：

のフーリエ変換はで与えられる：

に対する周波数応答はで与えられる：

フィルタはローパスフィルタである：

のフーリエ変換は で与えられる：

に対する周波数応答はで与えられる：

フィルタはローパスフィルタである：

のフーリエ変換は で与えられる：

おもしろい例題  (2)

スケーリング関数の平行移動と膨張をプロットする：

ウェーブレット関数の平行移動と膨張をプロットする：

Wolfram Research (2010), CDFWavelet, Wolfram言語関数， https://reference.wolfram.com/language/ref/CDFWavelet.html.

テキスト

Wolfram Research (2010), CDFWavelet, Wolfram言語関数， https://reference.wolfram.com/language/ref/CDFWavelet.html.

CMS

Wolfram Language. 2010. "CDFWavelet." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CDFWavelet.html.

APA

Wolfram Language. (2010). CDFWavelet. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CDFWavelet.html

BibTeX

@misc{reference.wolfram_2024_cdfwavelet, author="Wolfram Research", title="{CDFWavelet}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/CDFWavelet.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_cdfwavelet, organization={Wolfram Research}, title={CDFWavelet}, year={2010}, url={https://reference.wolfram.com/language/ref/CDFWavelet.html}, note=[Accessed: 18-November-2024 ]}