CDFWavelet

✖
`CDFWavelet`

✖

CDFWavelet[]

represents a Cohen–Daubechies–Feauveau wavelet of type "9/7".

✖

CDFWavelet["type"]

represents a Cohen–Daubechies–Feauveau wavelet of type "type".

Details

CDFWavelet defines a set of biorthogonal wavelets.
The following "type" forms can be used:
"5/3" used in lossless JPEG2000 compression

"9/7" used in lossy JPEG2000 compression
The scaling function (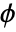) and wavelet function (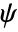) have compact support. The functions are symmetric.
CDFWavelet can be used with such functions as DiscreteWaveletTransform, WaveletPhi, etc.

Examples

open allclose all

Basic Examples (3)Summary of the most common use cases

Scaling function:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-gpi6tg

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-gb8f9b

Out[2]=2

Wavelet function:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-vc7o0g

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-xdbxfp

Out[2]=2

Filter coefficients:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-kjry2h

Out[1]=1

Scope (16)Survey of the scope of standard use cases

Basic Uses (10)

Compute primal lowpass filter coefficients:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-5q3vbl

Out[1]=1

Dual lowpass filter coefficients:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-8wgk6z

Out[1]=1

Primal highpass filter coefficients:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-ghmu0m

Out[1]=1

Dual highpass filter coefficients:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-5utoqa

Out[1]=1

Lifting filter coefficients:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-u5x0a9

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-1x7frz

Out[2]=2

Generate function to compute lifting wavelet transform:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-nfjqzn

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-ol7ejo

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-7bq5gu

Out[3]=3

Primal scaling function:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-1hi2ld

Out[1]=1

Dual scaling function:

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-cpb7tk

Out[2]=2

Plot scaling function using different levels of recursion:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-jvaues

Out[1]=1

Primal wavelet function:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-4fzw6t

Out[1]=1

Dual wavelet function:

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-pq6kvv

Out[2]=2

Plot scaling function using different levels of recursion:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-b0lb5q

Out[1]=1

Wavelet Transforms (5)

Compute a DiscreteWaveletTransform:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-xhbmxi

Out[1]=1

View the tree of wavelet coefficients:

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-gtqy6c

Out[2]=2

Get the dimensions of wavelet coefficients:

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-mrjnjd

Out[3]=3

Plot the wavelet coefficients:

In[4]:=4

✖

https://wolfram.com/xid/0fq4yj0wmxo02-qx915m

Out[4]=4

Compute a DiscreteWaveletPacketTransform:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-vtrxi2

Out[1]=1

View the tree of wavelet coefficients:

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-j3n0f1

Out[2]=2

Get the dimensions of wavelet coefficients:

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-wuwmcl

Out[3]=3

Plot the wavelet coefficients:

In[4]:=4

✖

https://wolfram.com/xid/0fq4yj0wmxo02-x0l386

Out[4]=4

Compute a StationaryWaveletTransform:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-lgbd1m

View the tree of wavelet coefficients:

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-jbb9sz

Out[2]=2

Get the dimensions of wavelet coefficients:

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-msff83

Out[3]=3

Plot the wavelet coefficients:

In[4]:=4

✖

https://wolfram.com/xid/0fq4yj0wmxo02-kn3y3t

Out[4]=4

Compute a StationaryWaveletPacketTransform:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-4fxpz9

View the tree of wavelet coefficients:

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-9rgpx

Out[2]=2

Get the dimensions of wavelet coefficients:

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-ngfrzh

Out[3]=3

Plot the wavelet coefficients:

In[4]:=4

✖

https://wolfram.com/xid/0fq4yj0wmxo02-b9yp0h

Out[4]=4

Compute a LiftingWaveletTransform:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-6vbut6

View the tree of wavelet coefficients:

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-xwj8z0

Out[2]=2

Get the dimensions of wavelet coefficients:

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-56ffkm

Out[3]=3

Plot the wavelet coefficients:

In[4]:=4

✖

https://wolfram.com/xid/0fq4yj0wmxo02-zrhgbc

Out[4]=4

Higher Dimensions (1)

Multivariate scaling and wavelet functions are products of univariate ones:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-rk8e1w

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-tvf11

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-yf2o9

Out[3]=3

In[4]:=4

✖

https://wolfram.com/xid/0fq4yj0wmxo02-s16yjj

Out[4]=4

In[5]:=5

✖

https://wolfram.com/xid/0fq4yj0wmxo02-gmiius

Out[5]=5

Properties & Relations (16)Properties of the function, and connections to other functions

Lowpass filter coefficients sum to unity; :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-v1t5fi

Out[1]=1

Highpass filter coefficients sum to zero; :

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-jrlqqz

Out[2]=2

Dual lowpass filter coefficients sum to unity; :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-80xeur

Out[1]=1

Dual highpass filter coefficients sum to zero; :

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-vggc8o

Out[2]=2

Scaling function integrates to unity; :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-3k44bm

Out[1]=1

Dual scaling function integrates to unity; :

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-50secc

Out[2]=2

Wavelet function integrates to zero; :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-7te20t

Out[1]=1

Dual wavelet function integrates to zero; :

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-cqbh6v

Out[2]=2

satisfies the recursion equation :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-yjbxzh

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-i0fiys

Plot the components and the sum of the recursion:

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-tb4pjl

In[4]:=4

✖

https://wolfram.com/xid/0fq4yj0wmxo02-wvsqxu

Out[4]=4

satisfies the recursion equation :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-32ph7g

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-lfizfd

Plot the components and the sum of the recursion:

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-pv65od

In[4]:=4

✖

https://wolfram.com/xid/0fq4yj0wmxo02-siy44p

Out[4]=4

satisfies the recursion equation :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-sr719e

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-761w33

Plot the components and the sum of the recursion:

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-bdrs22

In[4]:=4

✖

https://wolfram.com/xid/0fq4yj0wmxo02-ckzrbh

Out[4]=4

satisfies the recursion equation :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-4xlw98

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-seqsk7

Plot the components and the sum of the recursion:

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-or3keu

In[4]:=4

✖

https://wolfram.com/xid/0fq4yj0wmxo02-n5sx2h

Out[4]=4

Frequency response for is given by :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-y5x0mm

The filter is a lowpass filter:

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-za6vn3

Out[2]=2

Fourier transform of is given by :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-idptzz

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-4mxsvj

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-i4smhk

Out[3]=3

Frequency response for is given by :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-n4u9y2

The filter is a dual lowpass filter:

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-jod7ab

Out[2]=2

Fourier transform of is given by :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-le5e5v

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-qp24bt

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-ofeok2

Out[3]=3

Frequency response for is given by :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-6u603k

The filter is a lowpass filter:

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-3n6ywg

Out[2]=2

Fourier transform of is given by :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-b8inb0

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-vsncry

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-h8wifj

In[4]:=4

✖

https://wolfram.com/xid/0fq4yj0wmxo02-rzs5ol

Out[4]=4

Frequency response for is given by :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-sjcfi0

The filter is a lowpass filter:

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-my0oxb

Out[2]=2

Fourier transform of is given by :

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-69ezed

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-go2zbw

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-53vj8h

In[4]:=4

✖

https://wolfram.com/xid/0fq4yj0wmxo02-eytnvi

Out[4]=4

Neat Examples (2)Surprising or curious use cases

Plot translates and dilations of scaling function:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-yz9dxl

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-evsjio

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-p5xgws

Out[3]=3

Plot translates and dilations of wavelet function:

In[1]:=1

✖

https://wolfram.com/xid/0fq4yj0wmxo02-iu0uje

In[2]:=2

✖

https://wolfram.com/xid/0fq4yj0wmxo02-b9ooxs

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0fq4yj0wmxo02-hts69i

Out[3]=3

Top