CarlemanLinearize

CarlemanLinearize[sys,spec]

Carleman linearizes the nonlinear state-space model sys according to spec.

Details

  • CarlemanLinearize gives an approximation of the infinite order system in which sys is embedded.
  • For input-linear systems, the result is bilinear, that is, linear in both the states and inputs. In general, it is linear only in the states.
  • Possible values for spec:
  • kapproximation order
    {{e1,…,en}}monomials of the embedding transformation
    {…,{z1,…,zn}}new state variables
    {…,z,order}monomial ordering
  • Possible settings for order are the same as in MonomialList.
  • CarlemanLinearize returns a LinearizingTransformationData object that can be used to extract various properties.
  • The following properties can be given:
  • "EmbeddingTransformation"{z1->e1,…,zn->en}
    "TransformedSystem"approximate transformed system
    {"OriginalSystemController",κ}controller for the original system sys
    {"OriginalSystemEstimator",ℓ}estimator for the original system sys
    {"ClosedLoopSystem",κ}closed-loop system of sys with the controller

Examples

open allclose all

Basic Examples  (1)

Carleman linearize a nonlinear system:

Design a controller based on the linearized model:

The closed-loop system:

Simulate the closed-loop system:

Scope  (10)

Basic uses  (6)

Carleman linearize an affine system:

The transformed system is bilinear:

The embedding transformation:

Specify the new variables to use:

The results are now in terms of the specified variables:

Specify the terms of the transformation:

Specify the ordering:

Directly specify the property:

Multiple properties:

The linearization of a NonlinearStateSpaceModel:

The transformed system is linear in the states:

Properties  (4)

All properties:

Basic properties:

The transformation:

The transformed system:

Composite properties:

Linearize the system:

Design a controller based on the Taylor linearization of the transformed system:

The closed-loop system is a composite property:

The output response:

The controller for the original system:

The control effort:

The closed-loop system based on the Taylor linearization design:

The system's response:

Compare the two responses:

Design an estimator using Carleman linearization:

A set of estimator gains for the transformed system:

The estimator for the original system:

The trajectories of the estimated states:

The actual state trajectories:

Compare the actual and estimated state trajectories:

Applications  (2)

Design a therapy for HIV-1 infection based on Carleman linearization. The parameters are the decay rate and production rate of healthy cells, infection rate coefficient , and decay rate of the virus: »

The states are the levels of healthy cells and free virus , and the input is the drug dosage:

At the target level of 10, a low dosage results in increased virus levels:

Carleman linearize the system:

Design a controller for the linearized, higher-order system:

The closed-loop system:

The controller brings the healthy cell and virus concentrations to the desired levels:

The dosage level:

Design an estimator using Carleman linearization to estimate the reactant concentration based on the reactor temperature in a continuous stirred-tank reactor (CSTR): »

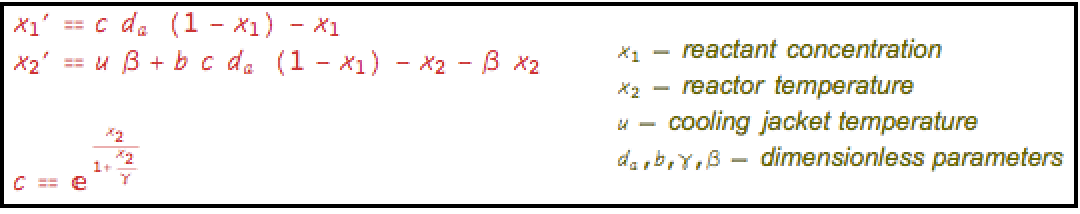
Assemble the model with as input and as states:

Carleman linearize the system:

Design an estimator:

Compute the actual reactant concentration:

Compare the actual and estimated values:

Properties & Relations  (1)

Carleman linearization of order 1:

It is equivalent to Taylor linearization:

Wolfram Research (2014), CarlemanLinearize, Wolfram Language function, https://reference.wolfram.com/language/ref/CarlemanLinearize.html.

Text

Wolfram Research (2014), CarlemanLinearize, Wolfram Language function, https://reference.wolfram.com/language/ref/CarlemanLinearize.html.

CMS

Wolfram Language. 2014. "CarlemanLinearize." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CarlemanLinearize.html.

APA

Wolfram Language. (2014). CarlemanLinearize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CarlemanLinearize.html

BibTeX

@misc{reference.wolfram_2024_carlemanlinearize, author="Wolfram Research", title="{CarlemanLinearize}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/CarlemanLinearize.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_carlemanlinearize, organization={Wolfram Research}, title={CarlemanLinearize}, year={2014}, url={https://reference.wolfram.com/language/ref/CarlemanLinearize.html}, note=[Accessed: 22-December-2024 ]}