WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

CarlsonRC

Carlsonの楕円積分を与える．

詳細

記号操作・数値操作の両方に適した数学関数である．
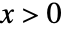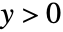かつのとき $TemplateBox[{x, y}, CarlsonRC]=1/2int_0^infty(t+x)^(-1/2)(t+y)^(-1)dt$ である．
CarlsonRC[x,y]は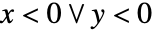に不連続な分枝切断線を持つ．
CarlsonRC[x,y]は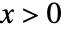，かつ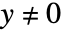で実数値である．これは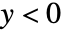，についてのコーシー(Cauchy)主値積分として解釈される．
特別な引数の場合，CarlsonRCは自動的に厳密値を計算する．
FunctionExpandは，適用可能な場合はCarlsonRCを初等関数に関する式に変換できる．
CarlsonRCは任意の数値精度で評価できる．
CarlsonRCは自動的にリストに縫い込まれる．
CarlsonRCは，IntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例 (3)

数値的に評価する：

関数をプロットする：

CarlsonRCはのときの特殊ケースのに関連している：

スコープ (13)

数値評価 (6)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素引数について評価する：

高精度で効率的に評価する：

CarlsonRCは要素単位でリストに縫い込まれる：

CarlsonRCは，IntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる．

特定の値 (2)

単純な厳密値は自動的に生成される：

FunctionExpandを使ってCarlsonRCを初等関数に変換する：

微分と積分 (2)

についてのの導関数：

についてのの導関数：

のについての不定積分：

のについての不定積分：

関数表現 (1)

TraditionalFormによる表示：

関数の恒等式と簡約 (2)

CarlsonRCは，オイラー・ポアソン(Euler–Poisson)の偏微分方程式を満足する：

CarlsonRCは，オイラーの同次関係を満足する：

アプリケーション (3)

CarlsonRCを使ってCarlsonRF[x,y,z]の上界と下界を与える：

CarlsonRCは，EllipticPiについてのパラメータ関係の変化をコンパクトに表すのに役に立つ：

CarlsonRCを使ってCarlsonRJについてのパラメータの変化を表す：

特性と関係 (3)

のとき，はArcCosによって表すことができる：

は，が負の実軸上にある場合はコーシー主値と解釈される：

正の引数についての同等の式と比較する：

FunctionExpandを使ってCarlsonRCをより簡単な関数で表す：

考えられる問題 (1)

一般にである．しかし，2つの関数の解析的な違いのために，評価は負の実軸上にはないの数値に限られる：

トップへ