CarlsonRE

CarlsonRE[x,y]

gives the Carlson's elliptic integral TemplateBox[{x, y}, CarlsonRE].

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • For non-negative arguments, TemplateBox[{x, y}, CarlsonRE]⩵1/piint_0^infty(t+x)^(-1/2)(t+y)^(-1/2)sqrt(t)( x/(t+x)+y/(t+y))dt.
  • CarlsonRE[x,y] has a branch cut discontinuity at .
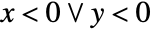  • For certain arguments, CarlsonRE automatically evaluates to exact values.
  • CarlsonRE can be evaluated to arbitrary numerical precision.
  • CarlsonRE automatically threads over lists.

Examples

open allclose all

Basic Examples  (3)

Evaluate numerically:

Plot the function:

CarlsonRE is related to Legendre's complete elliptic integral of the second kind:

Scope  (12)

Numerical Evaluation  (5)

Evaluate numerically:

Evaluate to high precision:

Precision of the output tracks the precision of the input:

Evaluate for complex arguments:

Evaluate efficiently at high precision:

CarlsonRE threads elementwise over lists:

Specific Values  (1)

Simple exact values are generated automatically:

Differentiation and Integration  (2)

Derivative with respect to :

Derivative with respect to :

Indefinite integral with respect to :

Indefinite integral with respect to :

Functional Representation  (1)

TraditionalForm formatting:

Function Identities and Simplifications  (3)

CarlsonRE satisfies the Euler–Poisson partial differential equation:

CarlsonRE satisfies Euler's homogeneity relation:

A partial differential equation satisfied by CarlsonRE:

Applications  (3)

Total arc length of an ellipse:

Compare with the result of ArcLength:

Expectation value of the square root of a quadratic form, relative to a normal distribution:

Compare with the closed-form result in terms of CarlsonRE:

Visualize the intersection of a cylinder and a ball:

Volume of cylinder-ball intersection expressed in terms of Carlson integrals:

Compare with the result of Volume:

Properties & Relations  (2)

CarlsonRE is invariant under a permutation of its arguments:

CarlsonRE and CarlsonRK satisfy Legendre's relation:

Wolfram Research (2021), CarlsonRE, Wolfram Language function, https://reference.wolfram.com/language/ref/CarlsonRE.html.

Text

Wolfram Research (2021), CarlsonRE, Wolfram Language function, https://reference.wolfram.com/language/ref/CarlsonRE.html.

CMS

Wolfram Language. 2021. "CarlsonRE." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CarlsonRE.html.

APA

Wolfram Language. (2021). CarlsonRE. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CarlsonRE.html

BibTeX

@misc{reference.wolfram_2024_carlsonre, author="Wolfram Research", title="{CarlsonRE}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/CarlsonRE.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_carlsonre, organization={Wolfram Research}, title={CarlsonRE}, year={2021}, url={https://reference.wolfram.com/language/ref/CarlsonRE.html}, note=[Accessed: 22-December-2024 ]}