Ceiling 
更多信息

- 数学函数,适合于符号和数值计算.
- Ceiling[x] 可以在 StandardForm 和 InputForm 中以 ⌈x⌉,
 lc
lc
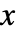
 rc
rc 或
或
\[LeftCeiling]x \[RightCeiling] 输入 ». - 当
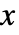 是任何数值量时,不论它是否为一个显式数字,Ceiling[x] 都返回整数.
是任何数值量时,不论它是否为一个显式数字,Ceiling[x] 都返回整数. - Ceiling 分别作用于复数的实部和虚部.
- 如果 a 不是正实数,Ceiling[x,a] 由公式 Ceiling[x,a]a Ceiling[x/a] 定义. »
- 对确切的数值量,Ceiling 在内部使用数值逼近求它的结果. 这个过程可以通过全局变量 $MaxExtraPrecision 的设置来改变.
- Ceiling 自动地线性作用于列表. »
范例
打开所有单元关闭所有单元
Wolfram Research (1988),Ceiling,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Ceiling.html (更新于 2007 年).
文本
Wolfram Research (1988),Ceiling,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Ceiling.html (更新于 2007 年).
CMS
Wolfram 语言. 1988. "Ceiling." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2007. https://reference.wolfram.com/language/ref/Ceiling.html.
APA
Wolfram 语言. (1988). Ceiling. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Ceiling.html 年