CoefficientArrays

CoefficientArrays[polys,vars]

得到多项式 polys 的变量 vars 的系数数组.

更多信息和选项

  • CoefficientArrays 给出包括对象 SparseArray 的列表，该对象可以用 Normal 转换成普通数组.
  • 若 CoefficientArrays[polys,vars] 给出 {m0,m1,m2,…}，则 polys 可重构为 m0+m1.vars+m2.vars.vars+…. »
  • polys 中形如 lhs==rhs 的任一元素对应于多项式 lhs-rhs. »
  • CoefficientArrays[polys,{form1,form2,…}] 取 polys 中与 formi 匹配的所有表达式作为变量.
  • CoefficientArrays[polys] 等价于 CoefficientArrays[polys,Variables[polys]].
  • CoefficientArrays[polys,vars] 的列表长度比 polys 的总次数高1.
  • mi 是秩为 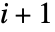的稀疏数组.
  • 第一个元素 m0 与 polys 列表的长度相同.
  • 若 polys 是一个多项式而不是列表，则 m0 也不是列表.
  • 对于线性方程，Thread[polys==0] 的解由 LinearSolve[m1,-m0] 给出.
  • 对于非线性方程，mi 不唯一. 在默认情况下，CoefficientArrays 只对变量与 vars 的次序相同的单项式赋予非零系数.
  • CoefficientArrays[polys,vars,"Symmetric"->True] 使得所有的 mi 在其指针中对称. 结果一般较不稀疏.

范例

打开所有单元关闭所有单元

基本范例  (1)

范围  (4)

线性多项式：

线性多项式列表：

非线性多项式：

多项式方程：

选项  (1)

"Symmetric"  (1)

对应于 y x 的二次形式的缺省系数是零：

当 "Symmetric"->True 时，CoefficientArrays 给出对称数组：

应用  (1)

转换线性方程为适合 LinearSolve 的数组：

属性和关系  (3)

可使用 Dot (.) 重构多项式：

对称系数数组对应于原点处的向量导数：

CoefficientArrays 给出根据总次数排序的多项式系数数组的列表：

CoefficientList 给出系数张量：

用 Coefficient 得到 的系数：

在 ca 中，此系数的位置是 a+b+1，随后是 a 个 1 和 b 个 2（1 和 2 表示第一个和第二个变量）：

在 cl 中, x^a y^b 的系数是位置在 {a+1,b+1} 的元素：

Wolfram Research (2003)，CoefficientArrays，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CoefficientArrays.html.

文本

Wolfram Research (2003)，CoefficientArrays，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CoefficientArrays.html.

CMS

Wolfram 语言. 2003. "CoefficientArrays." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/CoefficientArrays.html.

APA

Wolfram 语言. (2003). CoefficientArrays. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CoefficientArrays.html 年

BibTeX

@misc{reference.wolfram_2025_coefficientarrays, author="Wolfram Research", title="{CoefficientArrays}", year="2003", howpublished="\url{https://reference.wolfram.com/language/ref/CoefficientArrays.html}", note=[Accessed: 01-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_coefficientarrays, organization={Wolfram Research}, title={CoefficientArrays}, year={2003}, url={https://reference.wolfram.com/language/ref/CoefficientArrays.html}, note=[Accessed: 01-April-2025 ]}