CollinearPoints

CollinearPoints[{p1,p2,p3,…,pn}]

tests whether the points p1,p2,p3,…,pn are collinear.

Details

  • CollinearPoints is also known as rectilinear.
  • Typically used to test whether a set of points lie on the same straight line.
  • CollinearPoints[{p1,p2,p3,…,pn}] gives True if the points p3,…,pn are on the line passing through p1 and p2.
  • For collinear points p1, p2 and p3, the rank of the matrix {p2-p1,p3-p1} is less than or equal to 1.

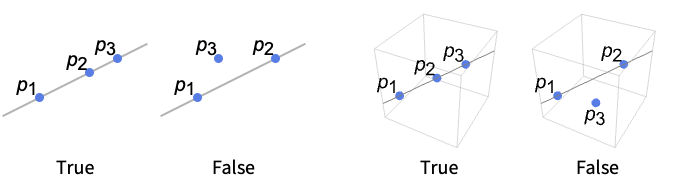
Examples

open allclose all

Basic Examples  (2)

The points {0,0},{1,2},{2,4} are collinear:

Plot the points:

Find the equation of the line passing through the points {0,1} and {1,2}:

Scope  (4)

CollinearPoints works with two-dimensional points:

Three-dimensional points:

-dimensional points:

CollinearPoints works with numerical coordinates:

Symbolic coordinates:

CollinearPoints over a set of coordinates:

List of points:

Multi-points:

CollinearPoints works for large sets:

Applications  (4)

Basic Applications  (3)

Find conditions for which two points lie on a line passing through the origin:

Explicit instances:

Find the equation of the line passing through the points {0,1} and {1,2}:

Draw collinear points:

Geometry  (1)

Noncollinear points form a polygon:

Collinear points:

Properties & Relations  (5)

PositivelyOrientedPoints returns False for collinear points:

NegativelyOrientedPoints returns False for collinear points:

Collinear points are coplanar:

Use RegionMember to test whether points are collinear:

Use InfiniteLine to draw a graphics image:

Wolfram Research (2020), CollinearPoints, Wolfram Language function, https://reference.wolfram.com/language/ref/CollinearPoints.html.

Text

Wolfram Research (2020), CollinearPoints, Wolfram Language function, https://reference.wolfram.com/language/ref/CollinearPoints.html.

CMS

Wolfram Language. 2020. "CollinearPoints." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CollinearPoints.html.

APA

Wolfram Language. (2020). CollinearPoints. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CollinearPoints.html

BibTeX

@misc{reference.wolfram_2025_collinearpoints, author="Wolfram Research", title="{CollinearPoints}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CollinearPoints.html}", note=[Accessed: 22-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_collinearpoints, organization={Wolfram Research}, title={CollinearPoints}, year={2020}, url={https://reference.wolfram.com/language/ref/CollinearPoints.html}, note=[Accessed: 22-February-2025 ]}