CoplanarPoints

CoplanarPoints[{p1,p2,p3,p4,…,pn}]

tests whether the points p1,p2,p3,p4,…,pn are coplanar.

Details

  • CoplanarPoints is also known as linearly dependent.
  • Typically used to test whether a set of points lie on the same plane.
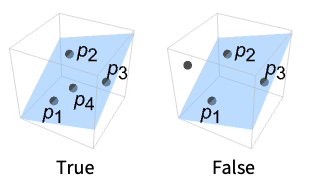
  • CoplanarPoints[{p1,p2,p3,p4,…,pn}] gives True if the points p4,…,pn are on the plane passing through the points p1, p2 and p3.
  • For coplanar points p1, p2, p3 and p4, the rank of the matrix {p2-p1,p3-p1,p4-p1} is less than or equal to 2.

Examples

open allclose all

Basic Examples  (2)

The points {0,0,0}, {1,1,-2}, {-1,2,-1}, {3,-4,1} are coplanar:

Plot the points:

Find the equation of the plane containing the points {0,0,0}, {1,1,-2} and {-1,2,-1}:

Scope  (4)

CoplanarPoints works with two-dimensional points:

Three-dimensional points:

n-dimensional points:

CoplanarPoints works with numerical coordinates:

Symbolic coordinates:

CoplanarPoints over a set of coordinates:

List of points:

Multi-points:

CoplanarPoints works for large sets:

Applications  (5)

Basic Applications  (4)

Find conditions for which two points lie on a plane passing through the origin:

Explicit instances:

2D points lie on the same plane:

Find the equation of a plane containing a set of points:

Draw coplanar points:

Geometry  (1)

A face of a polyhedron lies on a plane:

Properties & Relations  (5)

PositivelyOrientedPoints returns False for coplanar points:

NegativelyOrientedPoints returns False for coplanar points:

Collinear points are coplanar:

Use RegionMember to test whether points are coplanar:

Use InfinitePlane to draw a graphics image:

Wolfram Research (2020), CoplanarPoints, Wolfram Language function, https://reference.wolfram.com/language/ref/CoplanarPoints.html.

Text

Wolfram Research (2020), CoplanarPoints, Wolfram Language function, https://reference.wolfram.com/language/ref/CoplanarPoints.html.

CMS

Wolfram Language. 2020. "CoplanarPoints." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CoplanarPoints.html.

APA

Wolfram Language. (2020). CoplanarPoints. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CoplanarPoints.html

BibTeX

@misc{reference.wolfram_2024_coplanarpoints, author="Wolfram Research", title="{CoplanarPoints}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CoplanarPoints.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_coplanarpoints, organization={Wolfram Research}, title={CoplanarPoints}, year={2020}, url={https://reference.wolfram.com/language/ref/CoplanarPoints.html}, note=[Accessed: 18-November-2024 ]}