NegativelyOrientedPoints

NegativelyOrientedPoints[{p1,p2,p3,…,pn}]

tests whether the sequence of points p1,p2,p3,…,pn is negatively oriented.

Details

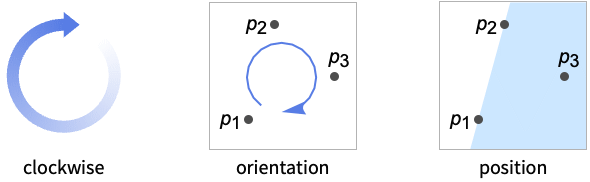
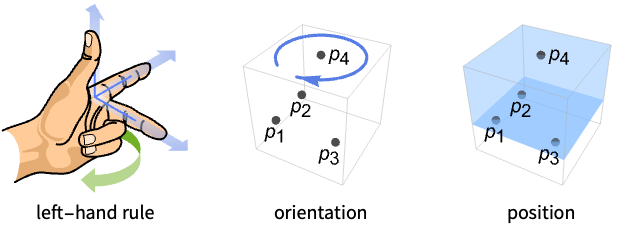
  • NegativelyOrientedPoints is also known as clockwise in 2D and left‐hand rule in 3D.
  • Typically used to determine the orientation of a rotational motion with respect to a set of points.
  • In two dimensions, NegativelyOrientedPoints[{p1,p2,p3}] gives True if the point p3 is in the half-plane bounded by the line through p1 and p2 and extended in the direction of {1,0}.
  • For negatively oriented points p1, p2 and p3, the determinant of the matrix {p2-p1, p3-p1} is negative.
  • In three dimensions, NegativelyOrientedPoints[{p1,p2,p3,p4}] gives True if the point p4 is in the half-space bounded by the plane through the point p1 with normal direction (p3-p1)(p2-p1).
  • For negatively oriented points p1, p2, p3 and p4, the dot product of p4-p1 and (p3-p1)(p2-p1) is negative.
  • In d dimensions, d+1 points p1,p2,…,pd+1 are negatively oriented if the determinant of the matrix {p2-p1,…,pd+1-p1} is negative.

Examples

open allclose all

Basic Examples  (2)

The points {0,0}, {1,1}, {.5,-1} are negatively oriented:

Plot the points:

Find the condition for which a point is below a plane:

Scope  (3)

NegativelyOrientedPoints works with two-dimensional points:

Three-dimensional points:

NegativelyOrientedPoints works with numerical coordinates:

Symbolic coordinates:

NegativelyOrientedPoints over a set of coordinates:

List of points:

Multi-points:

Generalizations & Extensions  (1)

Give assumptions to NegativelyOrientedPoints:

Applications  (5)

Basic Applications  (2)

Graph negatively oriented points:

Show the left-hand rule:

Geometry  (3)

Faces of a polyhedron are positively oriented:

NegativelyOrientedPoints over lines in 2D:

It is equivalent to the orientation of the consecutive vertices of the line:

Show the robustness of NegativelyOrientedPoints:

Properties & Relations  (4)

NegativelyOrientedPoints returns False for collinear points:

NegativelyOrientedPoints returns False if positively oriented:

Use RegionMember to test whether points are negatively oriented:

3D points are coplanar if they are neither positively nor negatively oriented:

Wolfram Research (2020), NegativelyOrientedPoints, Wolfram Language function, https://reference.wolfram.com/language/ref/NegativelyOrientedPoints.html.

Text

Wolfram Research (2020), NegativelyOrientedPoints, Wolfram Language function, https://reference.wolfram.com/language/ref/NegativelyOrientedPoints.html.

CMS

Wolfram Language. 2020. "NegativelyOrientedPoints." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NegativelyOrientedPoints.html.

APA

Wolfram Language. (2020). NegativelyOrientedPoints. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NegativelyOrientedPoints.html

BibTeX

@misc{reference.wolfram_2025_negativelyorientedpoints, author="Wolfram Research", title="{NegativelyOrientedPoints}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/NegativelyOrientedPoints.html}", note=[Accessed: 30-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_negativelyorientedpoints, organization={Wolfram Research}, title={NegativelyOrientedPoints}, year={2020}, url={https://reference.wolfram.com/language/ref/NegativelyOrientedPoints.html}, note=[Accessed: 30-July-2025 ]}