WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

CompleteIntegral[pde,u,{x1,…,xn}]

一階偏微分方程式 pde の完全積分 u を独立変数{x1,…,xn}を使って与える．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
アプリケーション  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

CompleteIntegral

CompleteIntegral[pde,u,{x1,…,xn}]

一階偏微分方程式 pde の完全積分 u を独立変数{x1,…,xn}を使って与える．

詳細とオプション

  • n 個の変数を持つ一階偏微分方程式の完全積分は，n 個の任意の独立定数 c1,c2,…,cnに依存する解である．
  • 完全積分は，通常，偏微分方程式の完全解集合を生成するために使われる．
  • 特定の初期条件を満足する偏微分方程式の解は，図示されているように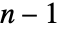，個のパラメータに依存する単純解の滑らかに変化する部分族の包絡線を構築することで得ることができる． »
  • CompleteIntegralからの出力は，DSolveにおけるのと同じように，従属関数 u または u[x1,…,xn]の形式によって制御される．
  • CompleteIntegralはSolveを使って陰的な解を与えることがある．
  • CompleteIntegralはInactive和や厳密には解けない積分を含む解を返すことがある．そのようなときには変数K[1], K[2], …が使われる．
  • 完全積分の任意の定数を含まない偏微分方程式の特殊解を得るために偏微分方程式の境界条件を指定することができる． »
  • 次は，使用可能なオプションである．
  • Assumptions$Assumptionsパラメータについての仮定
    GeneratedParametersC生成されたパラメータの命名方法
    MethodAutomatic使用するメソッド
  • GeneratedParametersは生成されたパラメータの形式を制御する．これらは，デフォルトで，定数C[n]である．

例題

すべて開く すべて閉じる

例  (3)

偏微分方程式の完全積分を求める：

Wolfram Language code: CompleteIntegral[D[u[x, y], x] - D[u[x, y], y] ^ 2 == Cos[x] , u[x, y], {x, y}]

任意の定数の特定の値について解をプロットする：

Wolfram Language code: Plot3D[u[x, y] /. %[[1]] /. {C[1] -> 1 / 3, C[2] -> 1}, {x, 0, 10Pi}, {y, 0, 5}]

wについて「純関数」完全積分を得る：

Wolfram Language code: CompleteIntegral[D[w[x, y], x] - y w[x, y]D[w[x, y], y] == w[x, y] + x ^ 2 - 1, w, {x, y}]

解を式に代入する：

Wolfram Language code: Simplify[D[w[x, y], x] - y w[x, y]D[w[x, y], y] == w[x, y] + x ^ 2 - 1 /. %]

三次元偏微分方程式の完全積分：

Wolfram Language code: CompleteIntegral[D[u[x, y, z], x] ^ 3 == D[u[x, y, z], y] + D[u[x, y, z], z], u[x, y, z], {x, y, z}]

条件を加える：

Wolfram Language code: CompleteIntegral[D[u[x, y, z], x] ^ 3 == D[u[x, y, z], y] + D[u[x, y, z], z] && u[0, 1, 1] == 1 && u[1, 0, 1] == 1 && u[0, 0, 1] == 1 / 2, u[x, y, z], {x, y, z}]

スコープ  (5)

二次元の偏微分方程式の完全積分を求める：

Wolfram Language code: CompleteIntegral[D[u[x, y], x] + D[u[x, y], y] == u[x, y] ^ 2, u[x, y], {x, y}]

uについて「純関数」完全積分を得る：

Wolfram Language code: CompleteIntegral[D[u[x, y], x] + D[u[x, y], y] == u[x, y] ^ 2, u, {x, y}]

解を式に代入する：

Wolfram Language code: Simplify[D[u[x, y], x] + D[u[x, y], y] /. %]

初等関数で表すことができる完全積分：

Wolfram Language code: CompleteIntegral[D[w[x, y], x] - 1 / Sin[y]w[x, y]D[w[x, y], y] == 1 / x w[x, y] + Log[x], w[x, y], {x, y}]

特殊関数で表すことができる完全積分：

Wolfram Language code: CompleteIntegral[D[w[x, y], x] - y w[x, y]D[w[x, y], y] == x w[x, y] + x ^ 2 - 1, w[x, y], {x, y}]

線形偏微分方程式の完全積分：

Wolfram Language code: CompleteIntegral[ D[u[x, y], x] - x D[u[x, y], y] == 0, u[x, y], {x, y}]

DSolveが与える解と比較する：

Wolfram Language code: DSolve[ D[u[x, y], x] - x D[u[x, y], y] == 0, u[x, y], {x, y}]

擬似線形偏微分方程式の完全積分：

Wolfram Language code: CompleteIntegral[ D[u[x, y], x] - u[x, y] D[u[x, y], y] == 0, u[x, y], {x, y}]

DSolveが与える解と比較する：

Wolfram Language code: DSolve[ D[u[x, y], x] - u[x, y] D[u[x, y], y] == 0, u[x, y], {x, y}]

アプリケーション  (2)

Clairautの方程式の完全積分を求める：

Wolfram Language code: ClairautEquation = u[x, y] == x * D[u[x, y], {x}] + y * D[u[x, y], {y}] + (1 / 2) * (D[u[x, y], {x}] ^ 2 + D[u[x, y], {y}] ^ 2);

完全積分は平面の2パラメータ族によって与えられる：

Wolfram Language code: csol = u[x, y] /. CompleteIntegral[ClairautEquation, u, {x, y}][[1]]

これらの平面の1パラメータ族を選択する：

Wolfram Language code: psol = csol /. {C[2] -> -1}

この平面の1パラメータ族の包絡線を求める：

Wolfram Language code: Solve[(D[psol, C[1]]) == 0, C[1]]
Wolfram Language code: envelope = psol /. %[[1]]//Together

包絡線も解であることを確認する：

Wolfram Language code: ClairautEquation /. {u -> Function[{x, y}, Evaluate[envelope]]}//Simplify

平面の1パラメータ族と包絡線解を可視化する：

Wolfram Language code: Animate[...]

ハミルトン(Hamilton)・ヤコビ(Jacobi)方程式の完全積分を求める：

Wolfram Language code: HamiltonJacobiEqn = D[u[t, x], t] + D[u[t, x], x] ^ 2 == 0;
Wolfram Language code: ci = CompleteIntegral[HamiltonJacobiEqn, u[t, x], {t, x}]

この方程式の包絡線解を計算する：

Wolfram Language code: sol = u[t, x] /. ci[[1]] /. {C[1] -> 0, C[2] -> a}
Wolfram Language code: Solve[D[sol, a] == 0, a]
Wolfram Language code: envelopsol = sol /. %[[1]]

包絡線解をプロットする：

Wolfram Language code: Plot3D[Evaluate[envelopsol], {t, -4, 4}, {x, -3, 3}, PlotRange -> All]

包絡線解が方程式を満足することを確認する：

Wolfram Language code: HamiltonJacobiEqn /. u -> Function[{t, x}, Evaluate[envelopsol]]

特性と関係  (2)

CompleteIntegralは非線形偏微分方程式の完全積分を求める：

Wolfram Language code: deqn = D[u[x, y], x] + D[u[x, y], y] ^ 2 == 1;
Wolfram Language code: CompleteIntegral[deqn, u[x, y], {x, y}]

DSolveは同じ解を警告メッセージとともに返す：

Wolfram Language code: DSolve[deqn, u[x, y], {x, y}]

CompleteIntegralを使って線形偏微分方程式の完全積分を求める：

Wolfram Language code: deqn = D[u[x, y], x] + D[u[x, y], y] == 1;
Wolfram Language code: CompleteIntegral[deqn, u[x, y], {x, y}]

DSolveはこの偏微分方程式の一般解を返す：

Wolfram Language code: DSolve[deqn, u[x, y], {x, y}]
Wolfram Research (2021), CompleteIntegral, Wolfram言語関数， https://reference.wolfram.com/language/ref/CompleteIntegral.html.

テキスト

Wolfram Research (2021), CompleteIntegral, Wolfram言語関数， https://reference.wolfram.com/language/ref/CompleteIntegral.html.

CMS

Wolfram Language. 2021. "CompleteIntegral." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CompleteIntegral.html.

APA

Wolfram Language. (2021). CompleteIntegral. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CompleteIntegral.html

BibTeX

@misc{reference.wolfram_2026_completeintegral, author="Wolfram Research", title="{CompleteIntegral}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/CompleteIntegral.html}", note=[Accessed: 06-July-2026]}

BibLaTeX

@online{reference.wolfram_2026_completeintegral, organization={Wolfram Research}, title={CompleteIntegral}, year={2021}, url={https://reference.wolfram.com/language/ref/CompleteIntegral.html}, note=[Accessed: 06-July-2026]}