WOLFRAM

Wolfram 语言与系统参考资料中心

CompleteIntegral[pde,u,{x1,…,xn}]

给出一阶偏微分方程 pde 的全积分 u，其中自变量为 {x1,…,xn}.

更多信息和选项
Details and Options Details and Options
范例  
基本范例  
范围  
应用  
属性和关系  
参见
相关指南
历史
按以下格式引用：

CompleteIntegral

CompleteIntegral[pde,u,{x1,…,xn}]

给出一阶偏微分方程 pde 的全积分 u，其中自变量为 {x1,…,xn}.

更多信息和选项

  • 具有 n 个变量的一阶偏微分方程 (PDE) 的全积分是依赖于 n 个独立任意常数 c1,c2,…,cn 的解.
  • 全积分通常用于生成 PDE 的完整解集.
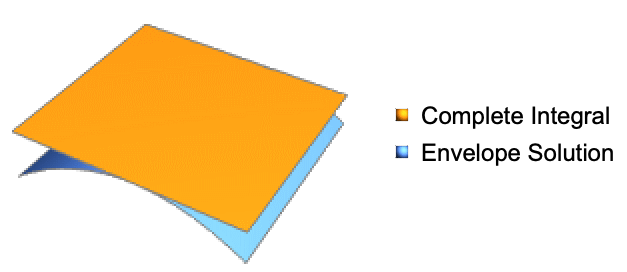
  • 满足特定初始条件的 PDE 的解可以通过构建依赖于 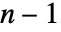个参数的简单解的平滑变化子族的包络来获得，如图所示. »
  • The output from CompleteIntegral 的输出由依赖函数 u 或 u[x1,…,xn] 控制，如在 DSolve 中一样.
  • CompleteIntegral 可以根据 Solve 给出隐式解.
  • CompleteIntegral 可以给出包含无法明确执行的 Inactive 和与积分的解. 在这种情况下使用变量 K[1], K[2], ….
  • 可以指定偏微分方程的边界条件以获得全积分中不受任意常数影响的偏微分方程的特解. »
  • 可以提供以下选项：
  • Assumptions$Assumptions参数假设
    GeneratedParametersC如何命名生成的参数
    MethodAutomatic使用什么方法
  • GeneratedParameters 控制生成参数的形式； 这些默认是常数 C[n].

范例

打开所有单元 关闭所有单元

基本范例  (3)

求偏微分方程的全积分：

Wolfram Language code: CompleteIntegral[D[u[x, y], x] - D[u[x, y], y] ^ 2 == Cos[x] , u[x, y], {x, y}]

绘制任意常数特定值的解：

Wolfram Language code: Plot3D[u[x, y] /. %[[1]] /. {C[1] -> 1 / 3, C[2] -> 1}, {x, 0, 10Pi}, {y, 0, 5}]

得到 w 的“纯函数”全积分：

Wolfram Language code: CompleteIntegral[D[w[x, y], x] - y w[x, y]D[w[x, y], y] == w[x, y] + x ^ 2 - 1, w, {x, y}]

将解代入表达式：

Wolfram Language code: Simplify[D[w[x, y], x] - y w[x, y]D[w[x, y], y] == w[x, y] + x ^ 2 - 1 /. %]

三维偏微分方程的全积分：

Wolfram Language code: CompleteIntegral[D[u[x, y, z], x] ^ 3 == D[u[x, y, z], y] + D[u[x, y, z], z], u[x, y, z], {x, y, z}]

现在添加条件：

Wolfram Language code: CompleteIntegral[D[u[x, y, z], x] ^ 3 == D[u[x, y, z], y] + D[u[x, y, z], z] && u[0, 1, 1] == 1 && u[1, 0, 1] == 1 && u[0, 0, 1] == 1 / 2, u[x, y, z], {x, y, z}]

范围  (5)

求二维偏微分方程的全积分：

Wolfram Language code: CompleteIntegral[D[u[x, y], x] + D[u[x, y], y] == u[x, y] ^ 2, u[x, y], {x, y}]

得到 u 的“纯函数”全积分：

Wolfram Language code: CompleteIntegral[D[u[x, y], x] + D[u[x, y], y] == u[x, y] ^ 2, u, {x, y}]

将解代入表达式：

Wolfram Language code: Simplify[D[u[x, y], x] + D[u[x, y], y] /. %]

可以用初等函数表示的全积分：

Wolfram Language code: CompleteIntegral[D[w[x, y], x] - 1 / Sin[y]w[x, y]D[w[x, y], y] == 1 / x w[x, y] + Log[x], w[x, y], {x, y}]

可以用特殊函数表示的全积分：

Wolfram Language code: CompleteIntegral[D[w[x, y], x] - y w[x, y]D[w[x, y], y] == x w[x, y] + x ^ 2 - 1, w[x, y], {x, y}]

线性偏微分方程的全积分：

Wolfram Language code: CompleteIntegral[ D[u[x, y], x] - x D[u[x, y], y] == 0, u[x, y], {x, y}]

与 DSolve 给出的解比较：

Wolfram Language code: DSolve[ D[u[x, y], x] - x D[u[x, y], y] == 0, u[x, y], {x, y}]

拟线性偏微分方程的全积分：

Wolfram Language code: CompleteIntegral[ D[u[x, y], x] - u[x, y] D[u[x, y], y] == 0, u[x, y], {x, y}]

与 DSolve 给出的解比较：

Wolfram Language code: DSolve[ D[u[x, y], x] - u[x, y] D[u[x, y], y] == 0, u[x, y], {x, y}]

应用  (2)

求 Clairaut 方程的全积分：

Wolfram Language code: ClairautEquation = u[x, y] == x * D[u[x, y], {x}] + y * D[u[x, y], {y}] + (1 / 2) * (D[u[x, y], {x}] ^ 2 + D[u[x, y], {y}] ^ 2);

全积分由两个参数的平面族给出：

Wolfram Language code: csol = u[x, y] /. CompleteIntegral[ClairautEquation, u, {x, y}][[1]]

选择这些平面的单参数族：

Wolfram Language code: psol = csol /. {C[2] -> -1}

求这个单参数平面族的包络：

Wolfram Language code: Solve[(D[psol, C[1]]) == 0, C[1]]
Wolfram Language code: envelope = psol /. %[[1]]//Together

验正该包络也是解：

Wolfram Language code: ClairautEquation /. {u -> Function[{x, y}, Evaluate[envelope]]}//Simplify

可视化单参数平面族和包络解：

Wolfram Language code: Animate[...]

求哈密顿-雅可比方程方程的全积分：

Wolfram Language code: HamiltonJacobiEqn = D[u[t, x], t] + D[u[t, x], x] ^ 2 == 0;
Wolfram Language code: ci = CompleteIntegral[HamiltonJacobiEqn, u[t, x], {t, x}]

计算方程的包络解：

Wolfram Language code: sol = u[t, x] /. ci[[1]] /. {C[1] -> 0, C[2] -> a}
Wolfram Language code: Solve[D[sol, a] == 0, a]
Wolfram Language code: envelopsol = sol /. %[[1]]

绘制包络解：

Wolfram Language code: Plot3D[Evaluate[envelopsol], {t, -4, 4}, {x, -3, 3}, PlotRange -> All]

验证包络解满足以下方程：

Wolfram Language code: HamiltonJacobiEqn /. u -> Function[{t, x}, Evaluate[envelopsol]]

属性和关系  (2)

CompleteIntegral 求非线性偏微分方程的全积分：

Wolfram Language code: deqn = D[u[x, y], x] + D[u[x, y], y] ^ 2 == 1;
Wolfram Language code: CompleteIntegral[deqn, u[x, y], {x, y}]

DSolve 返回带有警告消息的相同解：

Wolfram Language code: DSolve[deqn, u[x, y], {x, y}]

使用 CompleteIntegral 求线性偏微分方程的全积分：

Wolfram Language code: deqn = D[u[x, y], x] + D[u[x, y], y] == 1;
Wolfram Language code: CompleteIntegral[deqn, u[x, y], {x, y}]

DSolve 返回此偏微分方程的通解：

Wolfram Language code: DSolve[deqn, u[x, y], {x, y}]
Wolfram Research (2021)，CompleteIntegral，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CompleteIntegral.html.

文本

Wolfram Research (2021)，CompleteIntegral，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CompleteIntegral.html.

CMS

Wolfram 语言. 2021. "CompleteIntegral." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/CompleteIntegral.html.

APA

Wolfram 语言. (2021). CompleteIntegral. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CompleteIntegral.html 年

BibTeX

@misc{reference.wolfram_2026_completeintegral, author="Wolfram Research", title="{CompleteIntegral}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/CompleteIntegral.html}", note=[Accessed: 02-August-2026]}

BibLaTeX

@online{reference.wolfram_2026_completeintegral, organization={Wolfram Research}, title={CompleteIntegral}, year={2021}, url={https://reference.wolfram.com/language/ref/CompleteIntegral.html}, note=[Accessed: 02-August-2026]}