CompoundPoissonProcess

CompoundPoissonProcess[λ,jdist]

割合母数 λ でジャンプサイズ分布 jdist に従う複合ポアソン(Poisson)過程を表す．

詳細

  • CompoundPoissonProcessは，累積ポアソン過程あるいはポアソンクラスタ過程としても知られている．
  • CompoundPoissonProcessは連続時間で，jdist によって連続状態あるいは離散状態となるランダム過程である．
  • 時間 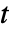における状態は 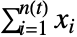で与えられる．ただし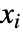，は jdist に従う独立同分布の確率変数であり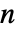， はPoissonProcess[λ]に従う．
  • 母数 λ は任意の正の実数でよく，jdist は任意の一変量分布でよい．
  • CompoundPoissonProcessは，Mean，Variance，RandomFunction等の関数で使うことができる．

例題

すべて開くすべて閉じる

例  (2)

指数ジャンプサイズ分布に従う複合ポアソン過程のシミュレーションを行う：

平均値関数と分散関数：

スコープ  (8)

基本的な用法  (4)

離散ジャンプがある複合ポアソン過程のシミュレーションを行う：

連続ジャンプがある複合ポアソン過程のシミュレーションを行う：

さまざまな更新率の複合ポアソン過程を比較する：

過程母数推定：

サンプルデータから分布母数を推定する：

過程スライス特性  (4)

スライス分布はCompoundPoissonDistributionである：

スライス分布のシミュレーションを行う：

スライス分布モーメント：

平均値関数：

分散関数：

歪度：

尖度：

スライス分布モーメントと母関数：

モーメント：

モーメント母関数：

キュムラント：

キュムラント母関数：

アプリケーション  (2)

改装開店した商店に，ポアソン過程に従って1時間に20人の割合で顧客が来店する．この商店は，販売促進の一環として，来店客全員に粗品を贈呈している．粗品の値は，形状母数10，尺度母数3のWeibullDistributionに従う．改装開店初日の営業時間である12時間について，粗品にかかる費用の過程のシミュレーションを行い，費用総額の期待値を求める：

過程のシミュレーションを12時間行う：

初日に贈られる粗品の費用総額の期待値：

粗品費用の分布のシミュレーションを行う：

費用分布の確率密度関数：

商店が500ドルから800ドルを粗品に費やす経験的確率：

リスクからの保険金請求総額は，ポアソン母数が200の複合ポアソン過程に従う．保険金請求額の分布は，最小値母数300，形状母数3，位置母数0のパレート(Pareto)分布に従う．保険業者は有効な保持レベル300の超過損害再保険に加入している．4年間の保険金請求の過程のシミュレーションを行う：

最初の4年間のスライス分布：

最初の4年間の再保険業者の保険金請求総額の平均と分散：

特性と関係  (6)

CompoundPoissonProcessはジャンプ過程である：

更新率 λ はジャンプの頻度を制御する：

複合ポアソン過程は弱定常ではない：

複合ポアソン過程の任意のスライス分布はCompoundPoissonDistributionである：

BernoulliDistributionの複合ポアソン過程のスライスはPoissonDistributionに従う：

特殊BorelTannerDistributionの複合ポアソン過程のスライスはPoissonConsulDistributionに従う：

Borel-Tanner分布に従う変数の和はBorel-Tanner分布に従うので，スライス分布はパラメータ混合分布と等しい：

特性関数と比較する：

Wolfram Research (2012), CompoundPoissonProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/CompoundPoissonProcess.html.

テキスト

Wolfram Research (2012), CompoundPoissonProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/CompoundPoissonProcess.html.

CMS

Wolfram Language. 2012. "CompoundPoissonProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CompoundPoissonProcess.html.

APA

Wolfram Language. (2012). CompoundPoissonProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CompoundPoissonProcess.html

BibTeX

@misc{reference.wolfram_2024_compoundpoissonprocess, author="Wolfram Research", title="{CompoundPoissonProcess}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CompoundPoissonProcess.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_compoundpoissonprocess, organization={Wolfram Research}, title={CompoundPoissonProcess}, year={2012}, url={https://reference.wolfram.com/language/ref/CompoundPoissonProcess.html}, note=[Accessed: 18-November-2024 ]}