WeibullDistribution

WeibullDistribution[α,β]

represents a Weibull distribution with shape parameter α and scale parameter β.

WeibullDistribution[α,β,μ]

represents a Weibull distribution with shape parameter α, scale parameter β, and location parameter μ.

Details

  • WeibullDistribution is also known as Rosin–Rammler distribution.
  • The probability density for value 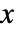in a Weibull distribution is proportional to 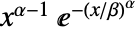for 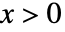, and is zero for . »
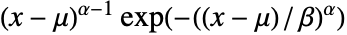  • The probability density for value in a Weibull distribution with location parameter is proportional to for 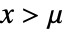, and is zero for .
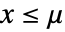  • WeibullDistribution allows α and β to be any positive real numbers and μ to be any real number.
  • WeibullDistribution allows β and μ to be any quantities of the same unit dimensions, and α to be a dimensionless quantity. »
  • WeibullDistribution can be used with such functions as Mean, CDF, and RandomVariate. »

Background & Context

  • WeibullDistribution[α,β,μ] represents a continuous statistical distribution supported on the interval 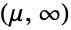and parametrized by a real number μ (called a "location parameter") and by positive real numbers α and β (a "shape parameter" and a "scale parameter", respectively), which together determine the overall behavior of its probability density function (PDF). Depending on the values of α, β, and μ, the PDF of a Weibull distribution may have any of a number of shapes, including unimodal with a single "peak" (i.e. a global maximum) or monotone decreasing with a potential singularity nearing the lower boundary of its domain. In addition, the tails of the PDF may be "fat" (i.e. the PDF decreases non-exponentially for large values ) or "thin" (i.e. the PDF decreases exponentially for large 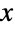), depending on the values of α, β, and μ. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Weibull distribution is sometimes referred to as the Rosin–Rammler distribution, and the two-parameter form WeibullDistribution[α,β] is equivalent to WeibullDistribution[α,β,0].
  • WeibullDistribution is one of four distributions (along with FrechetDistribution, ExtremeValueDistribution, and GumbelDistribution) classified under the general heading "extreme value distributions", all of which are used as tools for quantifying "extreme" or "rare" events (i.e. those that are "extremely unlikely", having datasets consisting of variates with extreme deviations from the median). The Weibull distribution is named for Swedish scientist Waloddi Weibull, though its discovery is due to Fréchet in the 1920s. Since its inception, the Weibull distribution has been used to model a number of real-world phenomena, including the distribution of particle sizes and wind speeds, as well as flood, drought, and catastrophic insurance losses. The Weibull distribution has also been used in survival analysis, manufacturing, engineering, and actuarial science.
  • RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Weibull distribution. Distributed[x,WeibullDistribution[α,β,μ]], written more concisely as xWeibullDistribution[α,β,μ], can be used to assert that a random variable x is distributed according to a Weibull distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
  • The probability density and cumulative distribution functions may be given using PDF[WeibullDistribution[α,β,μ],x] and CDF[WeibullDistribution[α,β,μ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
  • DistributionFitTest can be used to test if a given dataset is consistent with a Weibull distribution, EstimatedDistribution to estimate a Weibull parametric distribution from given data, and FindDistributionParameters to fit data to a Weibull distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Weibull distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Weibull distribution.
  • TransformedDistribution can be used to represent a transformed Weibull distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Weibull distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Weibull distributions.
  • WeibullDistribution is related to several other distributions. As mentioned previously, WeibullDistribution shares qualitative relationships with ExtremeValueDistribution, FrechetDistribution, and GumbelDistribution. These relationships can be quantified by noting that the PDF of WeibullDistribution can be realized as a transformation (TransformedDistribution) of ExtremeValueDistribution, FrechetDistribution, and GumbelDistribution. WeibullDistribution is a generalization of both ExponentialDistribution and RayleighDistribution, in the sense that the CDF of WeibullDistribution[1,1/λ] and the PDF of WeibullDistribution[2, σ], respectively, are equivalent to the CDF of ExponentialDistribution[λ] and the PDF of RayleighDistribution[σ], respectively. WeibullDistribution is also closely related to MinStableDistribution, MaxStableDistribution, GammaDistribution, and GompertzMakehamDistribution.

Examples

open allclose all

Basic Examples  (5)

Probability density function:

With location parameter:

Cumulative distribution function:

With location parameter:

Mean:

Variance:

Median:

Scope  (8)

Generate a sample of pseudorandom numbers from a Weibull distribution:

Compare its histogram to the PDF:

Distribution parameters estimation:

Estimate the distribution parameters from sample data:

Compare a density histogram of the sample with the PDF of the estimated distribution:

Skewness depends only on the first parameter:

The limiting value:

Kurtosis depends only on the first parameter:

Kurtosis attains minimum value:

The limiting value:

Different moments with closed forms as functions of parameters:

Moment:

Closed form for symbolic order:

CentralMoment:

FactorialMoment:

Cumulant:

Hazard function:

With location parameter:

Quantile function:

With location parameter:

Consistent use of Quantity in parameters yields QuantityDistribution:

Compute quartiles:

Applications  (8)

The lifetime of a component has WeibullDistribution with and given in . Find the probability that the component survives 300 hours:

Find the probability that the component is still working after 500 hours, after it has survived 300 hours:

Find the mean time to failure:

Simulate the failure times for 30 independent components like this:

The lifetime of a device has WeibullDistribution. Find the reliability of the device:

The hazard function is increasing in time for α>1 and any value of beta:

Find the reliability of two such devices in a series:

Find the reliability of two such devices in parallel:

Compare the reliability of both systems for and :

A component is manufactured in two factories. The products coming from factory A have a lifespan following Weibull distribution with and decades, while the time to failure for products coming from factory B follows Weibull distribution with and decades. Find the probability that a component from factory A fails before a component from factory B:

Assume 60% of components are being manufactured in factory A. Find the distribution of the time to failure of a randomly selected component:

Find the mean time to failure:

Compare the mean time to failure for each factory origin:

In the theory of fading channels, WeibullDistribution is used to model fading amplitude for mobile radio systems operating in the 800–900 MHz frequency range. Find the distribution of instantaneous signal-to-noise ratio where , is the energy per symbol, and is the spectral density of white noise:

Show is again a WeibullDistribution:

Find the mean:

Find the amount of fading:

Limiting values:

WeibullDistribution can be used to approximate wind speeds:

Find the estimated distribution:

Compare the PDF to the histogram of the wind data:

Find the probability of a day with wind speed greater than 30 km/h:

Find the mean wind speed:

Simulate daily average wind speeds for a month:

A site has mean wind speed 7 m/s and Weibull distribution with shape parameter 2:

The resulting wind speed distribution:

The power curve for a GE 1.5 MW wind turbine:

The total mean energy produced over the course of a year is then 4.3 GWh:

The magnitude of the annual maximum earthquake can be modeled using WeibullDistribution. Consider earthquakes in the United States in the past 200 years:

Find the annual maximum:

Create a sample, eliminating the missing data:

Fit Weibull distribution to the sample:

Compare the histogram of the sample with the PDF of the estimated distribution:

Using the model, find the probability of the annual maximum earthquake of magnitude at least 6:

Find the average magnitude of the annual maximum earthquake:

Simulate the magnitudes of the annual maximum earthquake for 30 years:

Find a stationary renewal distribution associated with a BenktanderWeibullDistribution:

Survival function:

Compare with a truncated WeibullDistribution:

Properties & Relations  (18)

Weibull distribution is closed under translation and scaling by a positive factor:

The family of WeibullDistribution is closed under minimum:

CDF of WeibullDistribution solves the minimum stability postulate equation:

Fix and and simplify:

A power of a WeibullDistribution is again a WeibullDistribution:

All moments are the same:

Compare PDFs through random sampling:

Relationships to other distributions:

The default location is 0:

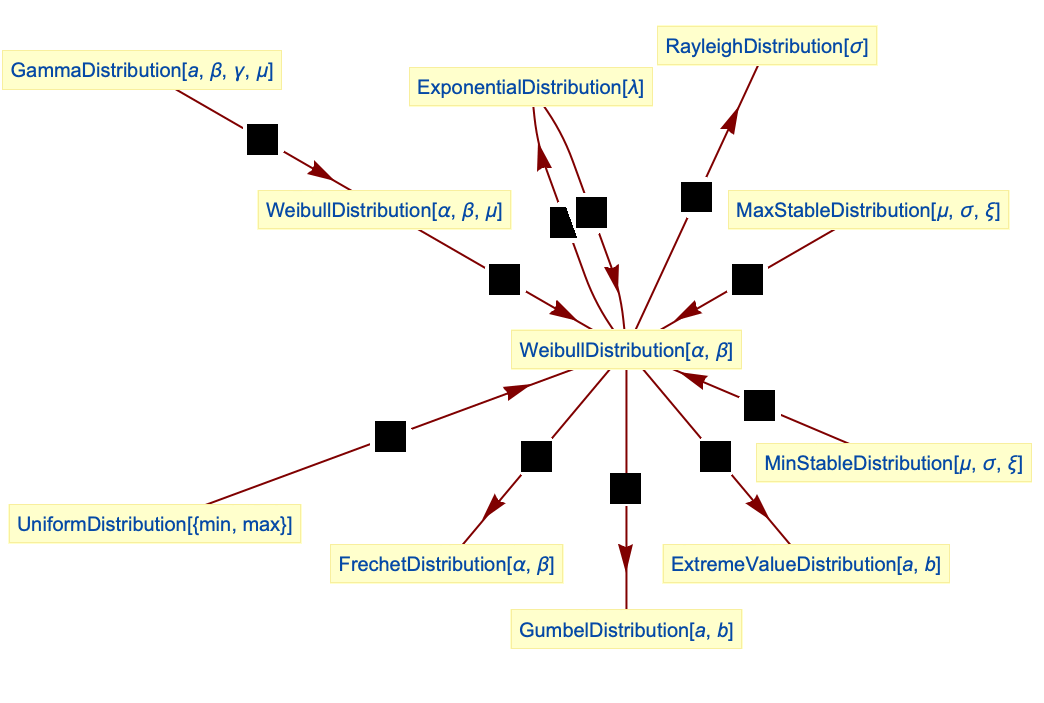
Weibull distribution is a transformation of UniformDistribution:

WeibullDistribution is exponentially related to ExtremeValueDistribution:

WeibullDistribution is exponentially related to GumbelDistribution:

ExponentialDistribution is a special case of Weibull distribution:

RayleighDistribution is a special case of Weibull distribution:

Weibull distribution is a transformation of ExponentialDistribution:

FrechetDistribution is a transformation of Weibull distribution:

Weibull distribution is a special case of MinStableDistribution:

Weibull distribution is a transformation of MaxStableDistribution:

WeibullDistribution is a special case of generalized GammaDistribution:

GompertzMakehamDistribution is related to truncated WeibullDistribution:

GompertzMakehamDistribution is related to Weibull distribution:

Possible Issues  (3)

WeibullDistribution is not defined when either α or β is not a positive real number:

The characteristic function of the Weibull distribution does not have a closed‐form representation:

Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:

Neat Examples  (1)

PDFs for different α values with CDF contours:

Wolfram Research (2007), WeibullDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/WeibullDistribution.html (updated 2016).

Text

Wolfram Research (2007), WeibullDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/WeibullDistribution.html (updated 2016).

CMS

Wolfram Language. 2007. "WeibullDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/WeibullDistribution.html.

APA

Wolfram Language. (2007). WeibullDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WeibullDistribution.html

BibTeX

@misc{reference.wolfram_2024_weibulldistribution, author="Wolfram Research", title="{WeibullDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/WeibullDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_weibulldistribution, organization={Wolfram Research}, title={WeibullDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/WeibullDistribution.html}, note=[Accessed: 22-November-2024 ]}