CompoundRenewalProcess

CompoundRenewalProcess[rdist,jdist]

再生時間分布 rdist，ジャンプサイズ分布 jdist の合成再生過程を表す．

詳細

  • CompoundRenewalProcessはまた，再生報酬過程あるいは累積再生過程としても知られている．
  • CompoundRenewalProcessは，連続 rdist の連続時間過程，離散 rdist の離散時間過程，連続 jdist の連続状態過程，そして離散 jdist の離散状態過程である．
  • 分布 rdist は非負の領域を持つ任意の一変量分布でよい．分布 jdist は任意の一変量分布でよい．
  • 時間 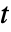における状態は 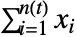で与えられる．ただし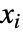， は独立同分布の確率変数で jdist に従い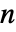， はRenewalProcess[jdist]に従う．
  • CompoundRenewalProcessは，Mean，Variance，RandomFunction等の関数で使うことができる．

例題

すべて開くすべて閉じる

例  (1)

ガンマ再生時間と指数ジャンプを持つ合成再生過程のシミュレーションを行う：

スコープ  (3)

離散ジャンプを持つ合成再生過程のシミュレーションを行う：

連続ジャンプを持つ合成再生過程のシミュレーションを行う：

過程母数推定：

サンプルデータから分布母数を推定する：

アプリケーション  (2)

改装開店した商店に，形状母数2，速度母数30のアーラン分布に従って顧客が来店する．この商店は，販売促進の一環として，来店客全員に粗品を贈呈している．粗品の値は，形状母数14，尺度母数3のWeibullDistributionに従う．改装開店初日の営業時間である12時間について，粗品にかかる費用の過程のシミュレーションを行い，費用総額の期待値を求める：

この過程のシミュレーションを12時間行う：

初日に贈られる粗品の費用総額の期待値：

粗品費用の分布のシミュレーションを行う：

経験的確率密度関数：

商店が450ドルから600ドルを粗品に費やす経験的確率：

ステップがNormalDistributionに従うランダムウォーク過程を定義する：

シミュレーションを行う：

平均値関数：

特性と関係  (3)

CompoundRenewalProcessはジャンプ過程である：

合成更新過程は弱定常ではない：

BinomialProcessは，合成更新過程の特殊ケースである：

平均値関数は一致する：

経験的共分散関数を作る：

共分散関数を比較する：

Wolfram Research (2012), CompoundRenewalProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html.

テキスト

Wolfram Research (2012), CompoundRenewalProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html.

CMS

Wolfram Language. 2012. "CompoundRenewalProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html.

APA

Wolfram Language. (2012). CompoundRenewalProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html

BibTeX

@misc{reference.wolfram_2024_compoundrenewalprocess, author="Wolfram Research", title="{CompoundRenewalProcess}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_compoundrenewalprocess, organization={Wolfram Research}, title={CompoundRenewalProcess}, year={2012}, url={https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html}, note=[Accessed: 18-November-2024 ]}