CompoundRenewalProcess

CompoundRenewalProcess[rdist,jdist]

表示一个复合更新过程，其中更新时间分布为 rdist，跳跃尺寸分布为 jdist.

更多信息

  • CompoundRenewalProcess 也被称为更新奖励过程或累积更新过程.
  • CompoundRenewalProcess 对于连续的 rdist，是连续时间过程，对于离散的 rdist，是离散时间过程，对于连续的 jdist，是连续状态过程，对于离散的 jdist，是离散状态过程.
  • 分布 rdist 是定义域为非负的任意单变量分布. 分布 jdist 可以是任意单变量分布.
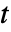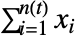  • 在时刻 的状态由 给出，其中 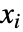是一个服从 jdist 的独立同分布随机变量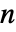， 服从 RenewalProcess[rdist].
  • CompoundRenewalProcess 可以与诸如 Mean、Variance 和 RandomFunction 等函数一起使用.

范例

打开所有单元关闭所有单元

基本范例  (1)

模拟一个复合更新过程，其中更新时间服从伽玛分布，跳跃服从指数分布：

范围  (3)

模拟一个具有离散跳跃的复合更新过程：

模拟一个具有连续跳跃的复合更新过程：

过程参数估计：

从样本数据估计分布参数：

应用  (2)

一家新装修好的商店举行酬宾活动，给每一位顾客都赠送一个礼品. 购物者每小时光顾这家商店的过程服从形状参数为2、速率参数为30的爱尔朗分布. 礼品价值服从 WeibullDistribution，其中形状参数为14，尺度参数为3. 模拟在该商店开业当天12小时内所赠送礼物的成本，并求总成本的期望值：

模拟12小时的过程：

开业当天赠出礼品的期望总成本：

模拟礼品成本分布：

经验概率密度函数：

这家商店的礼物花费在$450到$600之间的经验概率：

定义一个随机行走过程，其中步长服 NormalDistribution：

模拟：

均值函数：

属性和关系  (3)

CompoundRenewalProcess 是一个跳跃过程：

复合更新过程不是弱平稳的：

BinomialProcess 是复合更新过程的特殊情形：

均值函数一致：

创建经验协方差函数：

比较协方差函数：

Wolfram Research (2012)，CompoundRenewalProcess，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html.

文本

Wolfram Research (2012)，CompoundRenewalProcess，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html.

CMS

Wolfram 语言. 2012. "CompoundRenewalProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html.

APA

Wolfram 语言. (2012). CompoundRenewalProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html 年

BibTeX

@misc{reference.wolfram_2024_compoundrenewalprocess, author="Wolfram Research", title="{CompoundRenewalProcess}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_compoundrenewalprocess, organization={Wolfram Research}, title={CompoundRenewalProcess}, year={2012}, url={https://reference.wolfram.com/language/ref/CompoundRenewalProcess.html}, note=[Accessed: 18-November-2024 ]}