CoulombH1

CoulombH1[l,η,r]

gives the outgoing irregular Coulomb wavefunction TemplateBox[{l, eta, r}, CoulombH1].

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • CoulombH1[ℓ,η,r] is a solution of the ordinary differential equation .
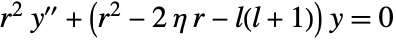  • CoulombH1[l,η,r] is proportional to 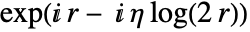for large .
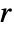  • CoulombH1[l,η,r] has a regular singularity at .
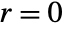  • CoulombH1 has a branch cut discontinuity in the complex 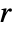plane running from 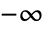to .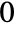
  • For certain special arguments, CoulombH1 automatically evaluates to exact values.
  • CoulombH1 can be evaluated to arbitrary numerical precision.
  • CoulombH1 automatically threads over lists.
  • CoulombH1 can be used with CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (5)

Evaluate numerically:

Evaluate to arbitrary precision:

CoulombH1 is a linear combination of the CoulombG and CoulombF functions:

Complex plot:

Symbolic evaluation for special parameters:

Asymptotic behavior at large radius:

Scope  (18)

Numerical Evaluation  (5)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

CoulombH1 can be used with CenteredInterval objects:

Specific Values  (3)

Limiting value at the origin:

For a zero value of the parameter η, CoulombH1 reduces to a spherical Hankel function:

Find the first positive zero of the real part of CoulombH1:

Visualization  (2)

Plot the real and imaginary parts of CoulombH1:

Plot the real part of TemplateBox[{2, 0, z}, CoulombH1]:

Plot the imaginary part of TemplateBox[{2, 0, z}, CoulombH1]:

Function Properties  (6)

Function domain of CoulombH1:

CoulombH1[2,0,x] is not injective over complexes:

CoulombH1[2,0,x] is neither non-negative nor non-positive:

CoulombH1[2,0,x] has both singularities and discontinuities:

CoulombH1 is neither convex nor concave:

TraditionalForm formatting:

Series Expansions  (1)

Find the Taylor expansion using Series at zero and at infinity:

Plots of the first three approximations for CoulombH1 around :

Function Representations  (1)

Relations with other Coulomb functions:

Properties & Relations  (1)

CoulombH1 is proportional to WhittakerW in some region of the complex plane:

However, the stated definition has a branch cut at , while the built-in CoulombH1 has a branch cut at :

Wolfram Research (2021), CoulombH1, Wolfram Language function, https://reference.wolfram.com/language/ref/CoulombH1.html (updated 2023).

Text

Wolfram Research (2021), CoulombH1, Wolfram Language function, https://reference.wolfram.com/language/ref/CoulombH1.html (updated 2023).

CMS

Wolfram Language. 2021. "CoulombH1." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/CoulombH1.html.

APA

Wolfram Language. (2021). CoulombH1. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CoulombH1.html

BibTeX

@misc{reference.wolfram_2025_coulombh1, author="Wolfram Research", title="{CoulombH1}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/CoulombH1.html}", note=[Accessed: 22-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_coulombh1, organization={Wolfram Research}, title={CoulombH1}, year={2023}, url={https://reference.wolfram.com/language/ref/CoulombH1.html}, note=[Accessed: 22-February-2025 ]}