CrossingPolygon

CrossingPolygon[{p₁,p₂,…,p_n}]

gives a Polygon representing all points for which a ray from the point in any direction in the plane crosses the line segments {p₁,p₂},…,{p_n-1,p_n},{p_n,p₁} an odd number of times.

CrossingPolygon[{{p₁₁,p₁₂,…},{p₂₁,p₂₂,…},…}]

gives a Polygon from the line segments {p₁₁,p₁₂},…,{p₂₁,p₂₂},….

Details and Options

CrossingPolygon is also known as even–odd filling rule.
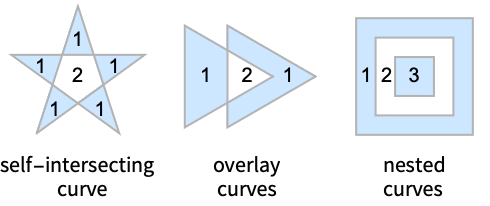
A point is in CrossingPolygon if a ray starting at that point to infinity in any direction will cross the boundary curves an odd number of times. The number of ray crossings is given by CrossingCount.
The number of ray crossings is given below for each region.

CrossingPolygon is used to define a polygon from possibly self-intersecting closed curves.

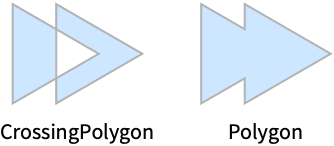
CrossingPolygon[{p₁,p₂,…,p_n}] is effectively equivalent to Polygon[{p₁,p₂,…,p_n}].
CrossingPolygon[{{p₁₁,p₁₂,…},{p₂₁,p₂₂,…},…}] is, in general, different than Polygon[{{p₁₁,p₁₂,…},{p₂₁,p₂₂,…},…}] since the former will use the ray crossing rule for all closed curves {p_i1,p_i2,…}. The latter is the union of polygons Polygon[{p_i1,p_i2,…}].

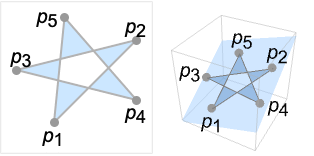
The points p_i can have any length but must all lie in a plane.
CrossingPolygon takes the same options as Polygon.

List of all options

Examples

open allclose all

Basic Examples (2)

Define a polygon:

Construct a polygon from a self-intersecting contour:

Compute its area:

Scope (11)

Basic Uses (5)

Define a 2-dimensional polygon:

Three-dimensional polygons:

-dimensional polygons:

Construct polygons from self-intersecting contours:

Multiple contours:

Self-Intersecting Contours (3)

CrossingPolygon works on self-intersecting contours:

Overlapping contour segments:

Multiple contours:

Multiple Contours (3)

CrossingPolygon works on multiple contours:

Intersecting contours:

Self-intersecting contours:

Options (6)

VertexColors (2)

Polygon with vertex colors:

Specify vertex colors for 3D polygons:

VertexNormals (1)

Compute normal vectors using the cross product of edge vectors:

A triangle with normals pointing in the direction {1,-1,1}:

Using different normals will affect shading:

VertexTextureCoordinates (3)

Texture mapping with 2D polygons:

Texture mapping with 3D polygons:

Repeat a texture by using non-unified texture coordinate values:

Texture mapping is preceded by VertexColors:

Applications (3)

Basic Applications (1)

Polygon construction from contours:

Computer Graphics (1)

Turtle drawing polygon. Advance 20 steps, always turning 110° toward the left:

Computational Geometry (1)

Generate random polygons:

Properties & Relations (3)

CrossingPolygon is effectively equivalent to Polygon for a single contour:

CrossingPolygon is, in general, different than Polygon for multiple intersecting contours:

WindingPolygon is an alternate polygon constructor:

Possible Issues (1)

The points in CrossingPolygon must all lie on a plane:

Neat Examples (1)

Digital petals:

Top