CrossingPolygon

CrossingPolygon[{p₁,p₂,…,p_n}]

给出表示一些点的 Polygon，在平面上从这些点出发的射线从任意方向上穿过线段 {p₁,p₂},…,{p_n-1,p_n},{p_n,p₁} 奇数次.

CrossingPolygon[{{p₁₁,p₁₂,…},{p₂₁,p₂₂,…},…}]

根据线段 {p₁₁,p₁₂},…,{p₂₁,p₂₂},… 给出 Polygon.

更多信息和选项

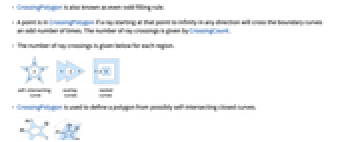
CrossingPolygon 也被称为奇偶填充规则.
如果从该点出发的射线从任意方向上穿过边界线奇数次，那么该点属于 CrossingPolygon. 射线交叉的次数由 CrossingCount 给出.
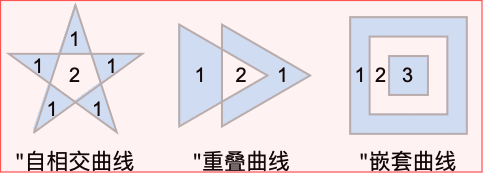
下面给出了每个区域的射线交叉次数.

CrossingPolygon 用于根据可能自相交的闭合曲线定义多边形.

CrossingPolygon[{p₁,p₂,…,p_n}] 实际上等价于 Polygon[{p₁,p₂,…,p_n}].
一般情况下，CrossingPolygon[{{p₁₁,p₁₂,…},{p₂₁,p₂₂,…},…}] 不同于 Polygon[{{p₁₁,p₁₂,…},{p₂₁,p₂₂,…},…}]，因为前者将对所有闭合曲线 {p_i1,p_i2,…} 使用射线交叉规则. 后者为多边形 Polygon[{p_i1,p_i2,…}] 的并集.

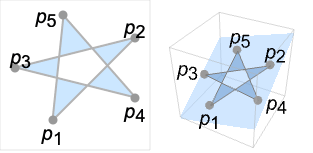
可有任意多个点 p_i，但必须都在一个平面上.
CrossingPolygon 接受与 Polygon 一样的选项.

所有选项的列表

范例

打开所有单元关闭所有单元

基本范例 (2)

定义一个多边形：

根据自相交轮廓线构建多边形：

计算其面积：

范围 (11)

基本用法 (5)

定义一个二维多边形：

三维多边形：

-维多边形：

根据自相交轮廓线构建多边形：

多个轮廓线：

自相交轮廓线 (3)

CrossingPolygon 适用于自相交轮廓线：

重叠轮廓线：

多个轮廓线：

多个轮廓线 (3)

CrossingPolygon 适用于多个轮廓线：

相交轮廓线：

自相交轮廓线：

选项 (6)

VertexColors (2)

顶点着色的多边形：

指定三维多边形的顶点的颜色：

VertexNormals (1)

用边向量的叉积计算法向量：

法线指向 {1,-1,1} 的三角形：

使用不同的法线将影响明暗：

VertexTextureCoordinates (3)

对 2D 多边形进行纹理映射：

对 3D 多边形进行纹理映射：

使用非统一纹理坐标值重复纹理：

纹理映射没有 VertexColors 的优先级高：

应用 (3)

基本应用 (1)

根据轮廓线构建多边形：

计算机图形 (1)

乌龟绘图. 前进 20 步，始终向左转 110°：

计算几何 (1)

生成随机多边形：

属性和关系 (3)

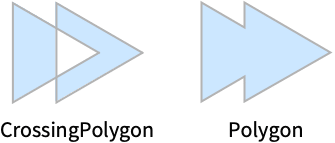
对于单轮廓线，CrossingPolygon 实际上等价于 Polygon：

一般情况下，对于多个相交轮廓线，CrossingPolygon 不同于 Polygon：

WindingPolygon 是另一个可用来构建多边形的函数：

可能存在的问题 (1)

CrossingPolygon 中的点必须位于一个平面上：

巧妙范例 (1)

数字花瓣：

顶部