CubeRoot[x]
gives the real-valued cube root of x.




CubeRoot
CubeRoot[x]
gives the real-valued cube root of x.
Details
- CubeRoot[x] returns the real-valued cube root for real-valued x.
- For symbolic x in CubeRoot[x], x is assumed to be real valued.
- CubeRoot can be evaluated to arbitrary numerical precision.
- CubeRoot automatically threads over lists.
- In StandardForm, CubeRoot[x] formats as
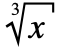 .
. 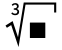 can be entered as
can be entered as  cbrt
cbrt .
.- ∛z can also be used for input. The ∛ character is entered as
 cbrti
cbrti or \[CubeRoot].
or \[CubeRoot].
Examples
open all close allBasic Examples (5)
Scope (36)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
CubeRoot threads elementwise over lists and matrices:
Compute average case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix CubeRoot function using MatrixFunction:
Specific Values (4)
Visualization (3)
Plot the CubeRoot function:
Visualize the absolute value and argument (sign) of ![]() :
:
The function ![]() has the same absolute value but a different argument for
has the same absolute value but a different argument for ![]() :
:
Function Properties (9)
CubeRoot is defined on the real numbers:
The range of CubeRoot is all real numbers:
Enter a ∛ character as \[CubeRoot], followed by a number:
![]() is neither non-negative nor non-positive:
is neither non-negative nor non-positive:
![]() is continuous on the reals but has a singularity at
is continuous on the reals but has a singularity at ![]() :
:
Differentiation (3)
Integration (4)
Series Expansions (4)
Find the Taylor expansion using Series:
Plots of the first three approximations around ![]() :
:
General term in the series expansion using SeriesCoefficient:
Function Identities and Simplifications (3)
Products can be combined using FullSimplify:
CubeRoot commutes with integer exponentiation:
Applications (1)
Solve a differential equation with CubeRoot:
Properties & Relations (5)
CubeRoot is only defined for real inputs:
CubeRoot is a bijection on the reals:
Use CubeRoot to find real cube roots:
Use Power[x,1/3] or ![]() to find the principal complex cube root:
to find the principal complex cube root:
The generating function for CubeRoot:
Find the integral of a function containing CubeRoot:
Visualize the function and the signed area between it and the ![]() axis:
axis:
Related Guides
Related Links
Text
Wolfram Research (2012), CubeRoot, Wolfram Language function, https://reference.wolfram.com/language/ref/CubeRoot.html (updated 2020).
CMS
Wolfram Language. 2012. "CubeRoot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/CubeRoot.html.
APA
Wolfram Language. (2012). CubeRoot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CubeRoot.html
BibTeX
@misc{reference.wolfram_2025_cuberoot, author="Wolfram Research", title="{CubeRoot}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CubeRoot.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_cuberoot, organization={Wolfram Research}, title={CubeRoot}, year={2020}, url={https://reference.wolfram.com/language/ref/CubeRoot.html}, note=[Accessed: 09-March-2026]}