CubeRoot

CubeRoot[x]

x の実数値の立方根を与える．

詳細

  • CubeRoot[x]は実数 x について実数値の立方根を与える．
  • CubeRoot[x]の記号 x については，x は実数値であると想定される．
  • CubeRootは任意の数値精度で評価することができる．
  • CubeRootは自動的にリストに縫い込まれる．
  • StandardFormでは，CubeRoot[x]は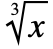と表される．
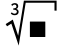  • は，cbrtで入力できる．
  • ∛z は入力に使うこともできる．∛ 記号はcbrtiあるいは\[CubeRoot]で入力する．

例題

すべて開くすべて閉じる

例  (5)

CubeRootは実数根を与える：

実数の部分集合上でプロットする：

cbrtを使ってを入力する：

これは(Power[x,1/3])と同じではない点に注意のこと：

との実部と虚部を実数上で比較する：

級数展開：

スコープ  (36)

数値評価  (6)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

高精度で効率よく評価する：

CubeRootは要素単位でリストと行列に縫い込まれる：

Aroundを使って平均的な場合の統計区間を計算する：

配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のCubeRoot関数を計算することもできる：

特定の値  (4)

固定点におけるCubeRootの値：

ゼロにおける値：

無限大における値：

Solveを使ってとなるような の値を求める：

結果を代入する：

結果を可視化する：

可視化  (3)

CubeRoot関数をプロットする：

の絶対値と引数(sign)を可視化する：

関数は について同じ絶対値を持つが，引数は異なる：

の極プロット：

関数の特性  (9)

CubeRootは実数について定義される：

CubeRootの範囲はすべての実数である：

∛ 記号を \[CubeRoot]として入力し，続けて数字を入力する：

は解析関数ではない：

は有理型でもない：

は非減少である：

は単射である：

全射でもある：

は非負でも非正でもない：

は実数上で連続であるが に特異点を持つ：

微分不可能なので特異なのである：


は凸でも凹でもない：

微分  (3)

x についての一次導関数：

x についての高次導関数：

x について高次導関数をプロットする：

x についての 次導関数の式：

積分  (4)

Integrateを使って不定積分を計算する：

不定積分を確かめる：

定積分：

対称区間上のCubeRootの定積分は0である：

その他の積分例：

級数展開  (4)

Seriesを使ってテイラー(Taylor)展開を求める：

の周りの最初の3つの近似をプロットする：

SeriesCoefficientを使った級数展開の一般項：

一次フーリエ(Fourier)級数：

生成点におけるテイラー(Taylor)展開：

関数の恒等式と簡約  (3)

主定義：

積はFullSimplifyを使って組み合せることができる：

CubeRootは整数指数と可換である：

アプリケーション  (1)

CubeRootを含む微分方程式を解く：

特性と関係  (5)

CubeRootは実数入力に対してしか定義されない：

CubeRootは実数上で全単射である：

CubeRootを使って実数の立方根を求める：

Power[x,1/3]またはを使って主複素立方根を求める：

CubeRootの母関数：

CubeRootを含む関数の積分を求める：

関数と，関数と 軸の間の符号付きの領域を可視化する：

考えられる問題  (1)

負の実軸上では，CubeRoot[x]はPower[x,1/3]によって返された主根とは異なる：

Wolfram Research (2012), CubeRoot, Wolfram言語関数， https://reference.wolfram.com/language/ref/CubeRoot.html （2020年に更新）.

テキスト

Wolfram Research (2012), CubeRoot, Wolfram言語関数， https://reference.wolfram.com/language/ref/CubeRoot.html （2020年に更新）.

CMS

Wolfram Language. 2012. "CubeRoot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/CubeRoot.html.

APA

Wolfram Language. (2012). CubeRoot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CubeRoot.html

BibTeX

@misc{reference.wolfram_2024_cuberoot, author="Wolfram Research", title="{CubeRoot}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CubeRoot.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_cuberoot, organization={Wolfram Research}, title={CubeRoot}, year={2020}, url={https://reference.wolfram.com/language/ref/CubeRoot.html}, note=[Accessed: 22-November-2024 ]}