CubeRoot

CubeRoot[x]

给出 x 的立方根.

更多信息

  • x 为实数时，CubeRoot[x] 返回实立方根.
  • 对于 CubeRoot[x] 中的符号式 x，假定 x 是实数.
  • CubeRoot 可以计算到任意数值精度.
  • CubeRoot 自动逐项作用于列表的各个元素.
  • 在 StandardForm 中，CubeRoot[x] 格式化为
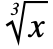
  • 可以通过 cbrt 输入 .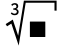
  • ∛z 也可用作输入. 可以通过 cbrti 或 \[CubeRoot]输入符号 ∛.

范例

打开所有单元关闭所有单元

基本范例  (5)

CubeRoot 给出实根：

在实数的子集上绘图：

使用 cbrt 输入 ：

注意它与 不同， 后者是 Power[x,1/3]：

在实数上比较 和 的实部和虚部：

级数展开：

范围  (36)

数值计算  (6)

数值化计算：

高精度计算：

输出的精度与输入的精度一致：

高精度的高效计算：

CubeRoot 按元素遍历列表和矩阵：

或用 Around 计算一般情况下的统计区间：

计算数组中每个元素的值：

或用 MatrixFunction 计算矩阵形式的 CubeRoot 函数：

特殊值  (4)

在固定点的 CubeRoot 的值：

零处的值：

无穷处的值：

用 Solve 求满足 的 值：

替换结果：

可视化结果：

可视化  (3)

绘制 CubeRoot 的函数：

可视化 的绝对值和辐角（符号）：

对于 ，函数 具有相同的绝对值但不同的辐角：

绘制 的极坐标图：

函数属性  (9)

CubeRoot 对实数有定义：

CubeRoot 的值域是全部实数：

通过 \[CubeRoot]输入 ∛，后面跟一个数字：

不是解析函数：

也不是亚纯函数：

非递减：

是单射函数：

也是满射函数：

既不是非负，也不是非正：

在实数上连续，但在 处有奇点：

在 处有奇点是因为它不可微：

既不凸，也不凹：

微分  (3)

关于 x 的一阶导：

关于 x 的高阶导：

绘制关于 x 的高阶导：

关于 x 的 阶导数的公式：

积分  (4)

使用 Integrate 计算不定积分：

验证反导数：

定积分：

CubeRoot 在对称区间上的定积分为 0：

更多积分：

级数展开  (4)

使用 Series 求泰勒展开：

绘制 附近的前三个近似：

用 SeriesCoefficient 获取计算展开式的通项：

一阶傅立叶级数：

普通点的泰勒展开：

函数恒等式与简化  (3)

主要定义：

乘积可以使用 FullSimplify 合并：

CubeRoot 与整数取幂互换：

应用  (1)

使用 CubeRoot 求解微分方程：

属性和关系  (5)

CubeRoot 只对实数有定义：

CubeRoot 在实数上是双射函数：

用 CubeRoot 求实立方根：

用 Power[x,1/3] 或 求复主立方根：

CubeRoot 的母函数：

求解包含 CubeRoot 的函数的积分：

可视化函数及其与 轴之间的有向面积：

可能存在的问题  (1)

在负实轴上，CubeRoot[x] 不同于由 Power[x,1/3] 返回的主根：

Wolfram Research (2012)，CubeRoot，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CubeRoot.html （更新于 2020 年）.

文本

Wolfram Research (2012)，CubeRoot，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CubeRoot.html （更新于 2020 年）.

CMS

Wolfram 语言. 2012. "CubeRoot." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/CubeRoot.html.

APA

Wolfram 语言. (2012). CubeRoot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CubeRoot.html 年

BibTeX

@misc{reference.wolfram_2024_cuberoot, author="Wolfram Research", title="{CubeRoot}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CubeRoot.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_cuberoot, organization={Wolfram Research}, title={CubeRoot}, year={2020}, url={https://reference.wolfram.com/language/ref/CubeRoot.html}, note=[Accessed: 22-November-2024 ]}