DEigensystem
✖
DEigensystem
詳細とオプション

- DEigensystemは,指定された境界条件を持つ常微分演算子および偏微分演算子について,固有値と固有関数を計算することができる.
- DEigensystemは,固有値 λiと固有関数 uiのリスト{{λ1,…,λn},{u1,…,un}}を与える.
- 微分演算子 ℒ についての固有値と固有関数のペア{λi,ui}は,ℒ[ui[x,y,…]]==λi ui[x,y,…]を満足する.
- 同次DirichletCondition境界条件あるいは同次NeumannValue境界条件が含まれることがある.非同次境界条件は対応する同次境界条件で置換される
- 境界 ∂Ωについて境界条件が指定されていない場合は,ノイマン(Neumann)0条件を指定することに等しい.
- 方程式 eqns はDSolveにおけるように指定される.
- N[DEigensystem[…]]は,記号的に計算できない固有系についてはNDEigensystemを呼び出す.
- 使用可能なオプション
-
Assumptions $Assumptions パラメータについての仮定 Method Automatic 使用するメソッド - 固有関数は自動的には正規化されない.Method->"Normalize"の設定を使って正規化された固有関数を使うことができる.
例題
すべて開くすべて閉じる例 (2)基本的な使用例
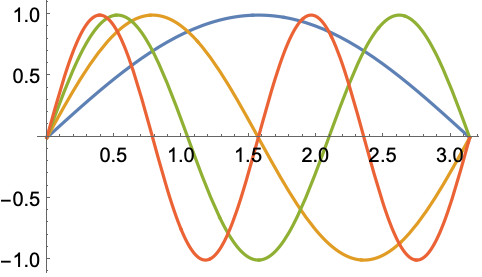
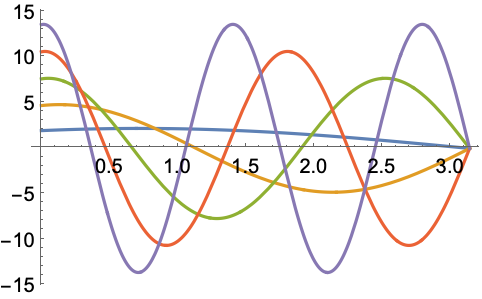
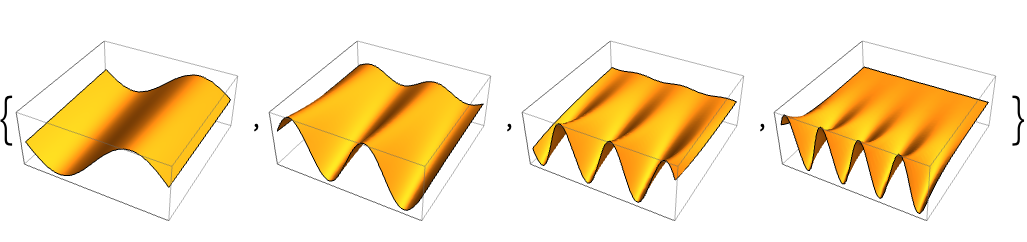
[0,π]上で,ラプラス(Laplace)演算子の最も小さい4つの固有値と固有関数を求める:
https://wolfram.com/xid/0btnz7gc2iv2-yzdn77
https://wolfram.com/xid/0btnz7gc2iv2-wx5bbs
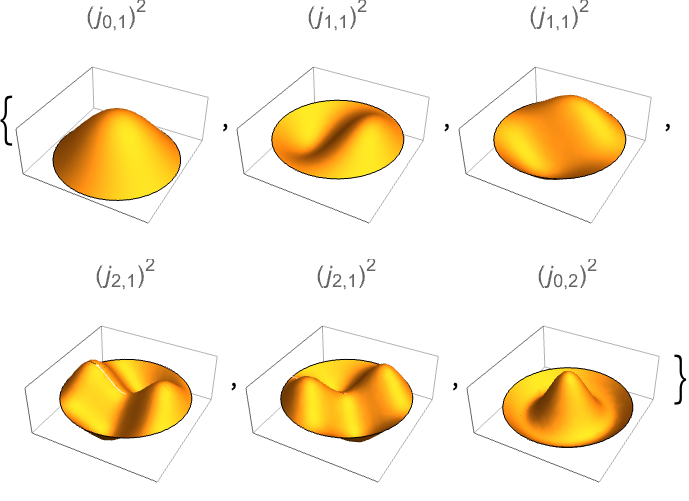
辺を固定した円筒膜について,最初の6つの固有関数を計算する:
https://wolfram.com/xid/0btnz7gc2iv2-d3ex
https://wolfram.com/xid/0btnz7gc2iv2-crtyb1
https://wolfram.com/xid/0btnz7gc2iv2-q0978
スコープ (20)標準的な使用例のスコープの概要
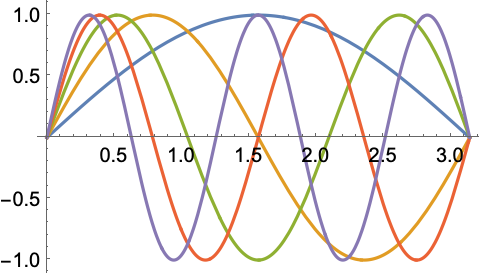
1D (9)
https://wolfram.com/xid/0btnz7gc2iv2-dd5aze
https://wolfram.com/xid/0btnz7gc2iv2-yjqx5u
https://wolfram.com/xid/0btnz7gc2iv2-b0b4f6
https://wolfram.com/xid/0btnz7gc2iv2-cvvh62
https://wolfram.com/xid/0btnz7gc2iv2-ge4exl
https://wolfram.com/xid/0btnz7gc2iv2-2d8bfg
https://wolfram.com/xid/0btnz7gc2iv2-kocy8b
https://wolfram.com/xid/0btnz7gc2iv2-v0oeps
https://wolfram.com/xid/0btnz7gc2iv2-3z82ab
https://wolfram.com/xid/0btnz7gc2iv2-ew1oj0
https://wolfram.com/xid/0btnz7gc2iv2-snvhso
https://wolfram.com/xid/0btnz7gc2iv2-cuzc9o
https://wolfram.com/xid/0btnz7gc2iv2-c9q6xh
https://wolfram.com/xid/0btnz7gc2iv2-bg0i4l
https://wolfram.com/xid/0btnz7gc2iv2-c5axvx
https://wolfram.com/xid/0btnz7gc2iv2-jy4ton
https://wolfram.com/xid/0btnz7gc2iv2-eb28a
https://wolfram.com/xid/0btnz7gc2iv2-u46ab
https://wolfram.com/xid/0btnz7gc2iv2-e05awx
https://wolfram.com/xid/0btnz7gc2iv2-hm0vt3
https://wolfram.com/xid/0btnz7gc2iv2-lya86
https://wolfram.com/xid/0btnz7gc2iv2-nsdqid
https://wolfram.com/xid/0btnz7gc2iv2-id4r85
https://wolfram.com/xid/0btnz7gc2iv2-cldpj3
https://wolfram.com/xid/0btnz7gc2iv2-essb5
https://wolfram.com/xid/0btnz7gc2iv2-by1ifr
https://wolfram.com/xid/0btnz7gc2iv2-cnfmi7
https://wolfram.com/xid/0btnz7gc2iv2-iqi360
https://wolfram.com/xid/0btnz7gc2iv2-lzzgzu
https://wolfram.com/xid/0btnz7gc2iv2-bzyyfz
https://wolfram.com/xid/0btnz7gc2iv2-di935k
https://wolfram.com/xid/0btnz7gc2iv2-d60btu
https://wolfram.com/xid/0btnz7gc2iv2-jy8mb2
https://wolfram.com/xid/0btnz7gc2iv2-cdj4k3
https://wolfram.com/xid/0btnz7gc2iv2-gdd6d0
https://wolfram.com/xid/0btnz7gc2iv2-j8g1rh
https://wolfram.com/xid/0btnz7gc2iv2-33s8q5
https://wolfram.com/xid/0btnz7gc2iv2-gjib28
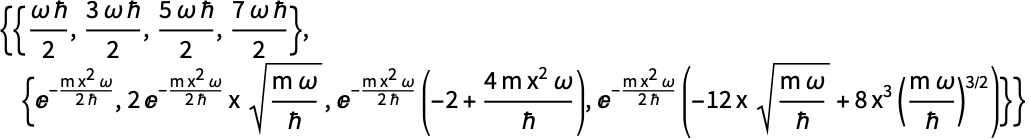
https://wolfram.com/xid/0btnz7gc2iv2-mzmdbz
https://wolfram.com/xid/0btnz7gc2iv2-1dfazx
https://wolfram.com/xid/0btnz7gc2iv2-ribue
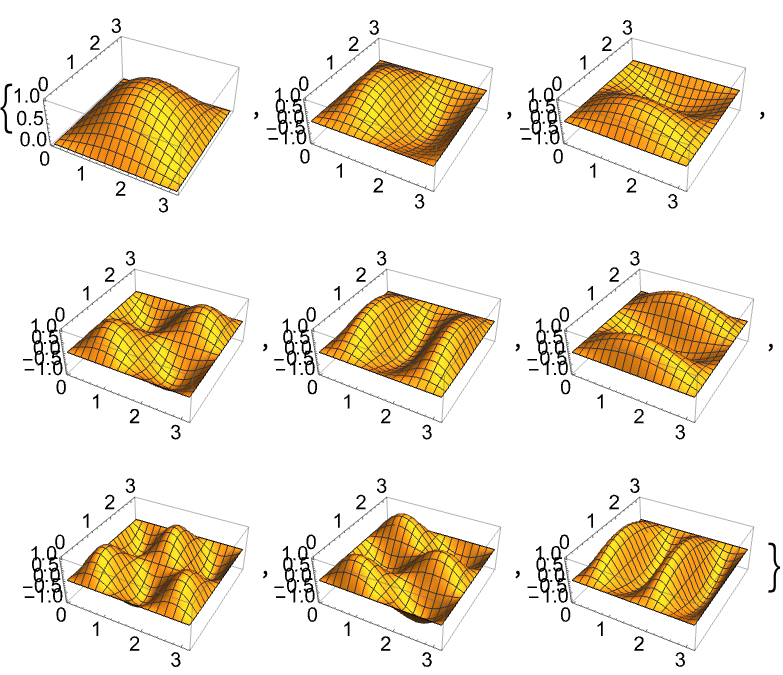
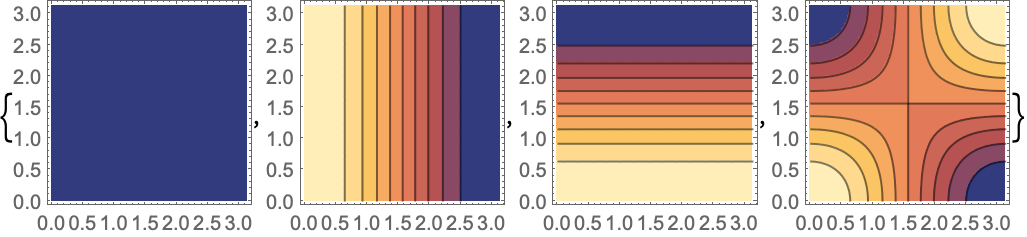
2D (6)
https://wolfram.com/xid/0btnz7gc2iv2-olvz0
https://wolfram.com/xid/0btnz7gc2iv2-q0svtk
https://wolfram.com/xid/0btnz7gc2iv2-yhxj38
https://wolfram.com/xid/0btnz7gc2iv2-ey9fmu
https://wolfram.com/xid/0btnz7gc2iv2-dzc5oc
https://wolfram.com/xid/0btnz7gc2iv2-3cf8zi
https://wolfram.com/xid/0btnz7gc2iv2-qpg6gs
https://wolfram.com/xid/0btnz7gc2iv2-snrji
https://wolfram.com/xid/0btnz7gc2iv2-hz8azd
https://wolfram.com/xid/0btnz7gc2iv2-sq6djy
https://wolfram.com/xid/0btnz7gc2iv2-tzp4z
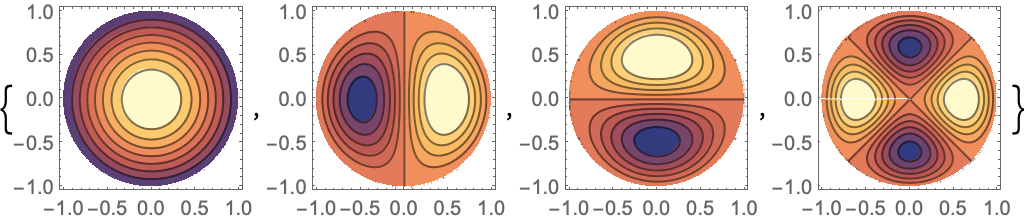
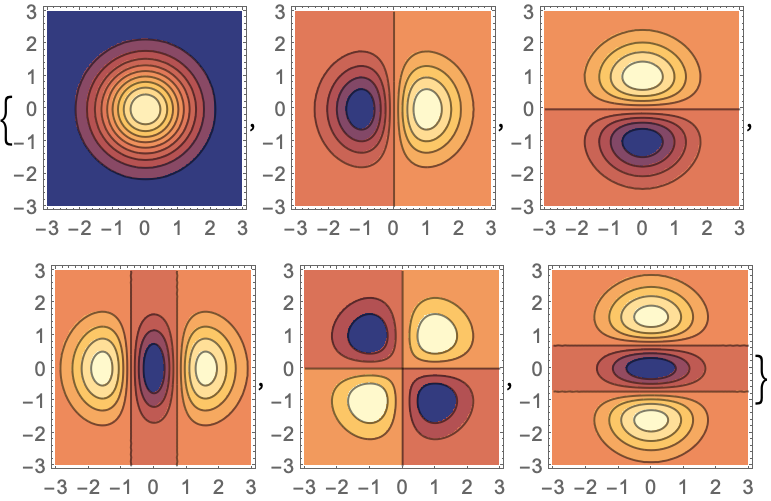
演算子の最も小さい4つの固有値と固有関数を単位円板上で求める:
https://wolfram.com/xid/0btnz7gc2iv2-646c3s
https://wolfram.com/xid/0btnz7gc2iv2-4ir027
https://wolfram.com/xid/0btnz7gc2iv2-dvcswe
https://wolfram.com/xid/0btnz7gc2iv2-x4itsm
https://wolfram.com/xid/0btnz7gc2iv2-mdxmrr
https://wolfram.com/xid/0btnz7gc2iv2-tdyb7u
https://wolfram.com/xid/0btnz7gc2iv2-vmgimx
https://wolfram.com/xid/0btnz7gc2iv2-wiu9y7
https://wolfram.com/xid/0btnz7gc2iv2-calu3w
https://wolfram.com/xid/0btnz7gc2iv2-bs5esh
演算子の最も小さい6つの演算子の固有値と固有関数を三角形内で求める:
https://wolfram.com/xid/0btnz7gc2iv2-bwxx0l
https://wolfram.com/xid/0btnz7gc2iv2-l49dkt
https://wolfram.com/xid/0btnz7gc2iv2-bp7icj
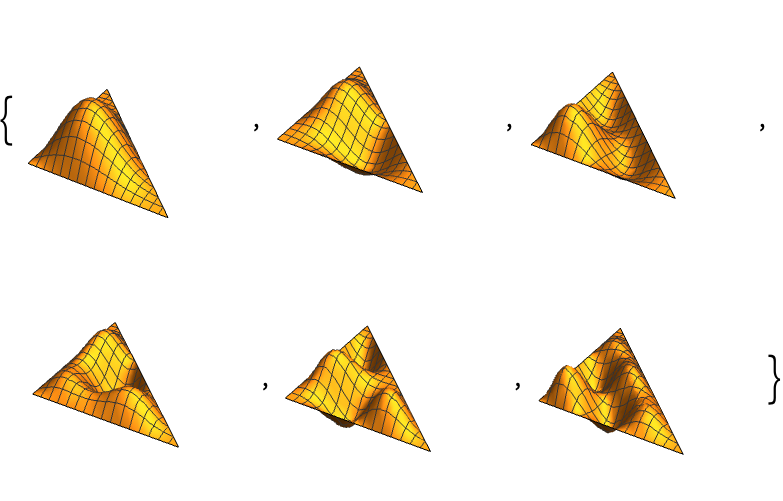
https://wolfram.com/xid/0btnz7gc2iv2-hqm92
https://wolfram.com/xid/0btnz7gc2iv2-kd8b62
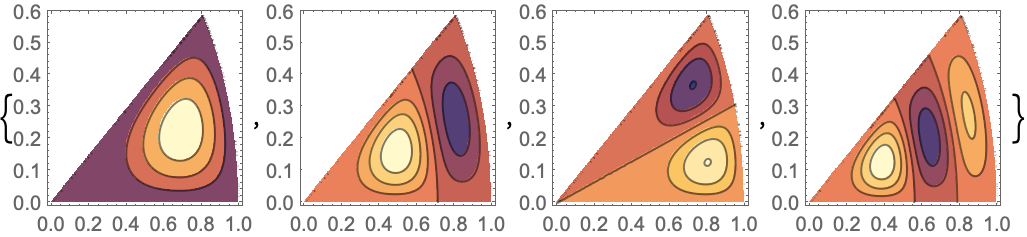
演算子の最も小さい4つの固有値と固有関数を円板のセクター上で求める:
https://wolfram.com/xid/0btnz7gc2iv2-fc0694
https://wolfram.com/xid/0btnz7gc2iv2-b0jk9w
https://wolfram.com/xid/0btnz7gc2iv2-lyqv9v
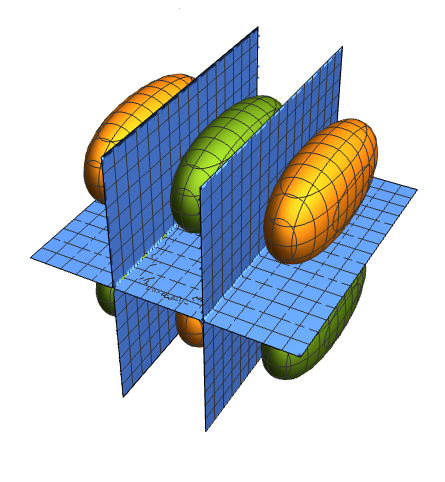
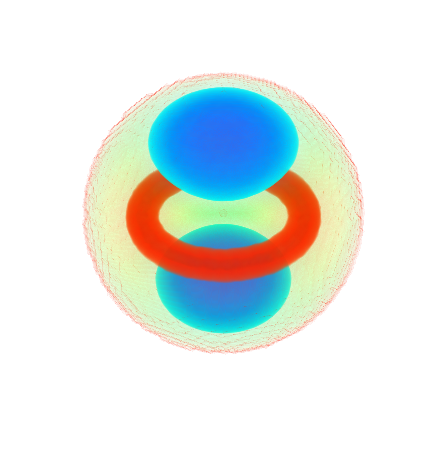
3D (5)
https://wolfram.com/xid/0btnz7gc2iv2-5soch
https://wolfram.com/xid/0btnz7gc2iv2-idhpb
https://wolfram.com/xid/0btnz7gc2iv2-lqu653
https://wolfram.com/xid/0btnz7gc2iv2-beoef7
https://wolfram.com/xid/0btnz7gc2iv2-coor33
https://wolfram.com/xid/0btnz7gc2iv2-d0ilyf
https://wolfram.com/xid/0btnz7gc2iv2-i9ulj9
https://wolfram.com/xid/0btnz7gc2iv2-jo5954
https://wolfram.com/xid/0btnz7gc2iv2-c137sl
https://wolfram.com/xid/0btnz7gc2iv2-4wlns

https://wolfram.com/xid/0btnz7gc2iv2-chbrb7
https://wolfram.com/xid/0btnz7gc2iv2-cwisu0
https://wolfram.com/xid/0btnz7gc2iv2-j6wop0
https://wolfram.com/xid/0btnz7gc2iv2-bhg57v
https://wolfram.com/xid/0btnz7gc2iv2-hhf5pu
https://wolfram.com/xid/0btnz7gc2iv2-tdyqt
https://wolfram.com/xid/0btnz7gc2iv2-j4mv75
https://wolfram.com/xid/0btnz7gc2iv2-jct22c

https://wolfram.com/xid/0btnz7gc2iv2-bewipj
https://wolfram.com/xid/0btnz7gc2iv2-o98g3b
https://wolfram.com/xid/0btnz7gc2iv2-8oi6tm
https://wolfram.com/xid/0btnz7gc2iv2-gp270a
https://wolfram.com/xid/0btnz7gc2iv2-evmcm5
https://wolfram.com/xid/0btnz7gc2iv2-2klld7
オプション (2)各オプションの一般的な値と機能
Assumptions (1)
Assumptionsを使って結果を簡約する:
https://wolfram.com/xid/0btnz7gc2iv2-ecanzm
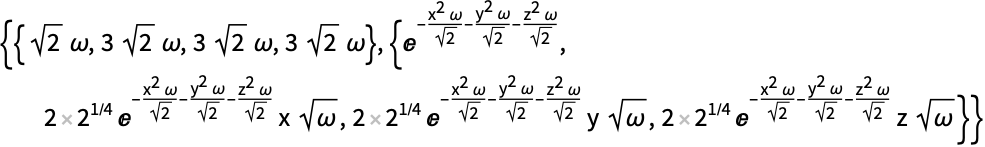
オプションがないと,等しくはあるがより複雑な答が返されるだろう:
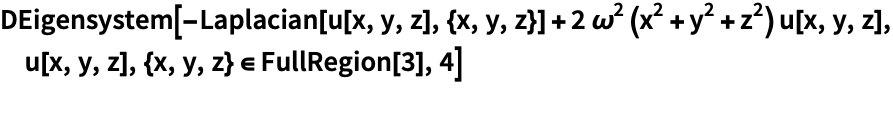
https://wolfram.com/xid/0btnz7gc2iv2-yyrzi2
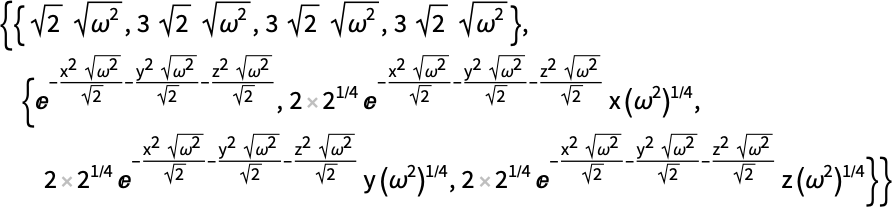
アプリケーション (3)この関数で解くことのできる問題の例
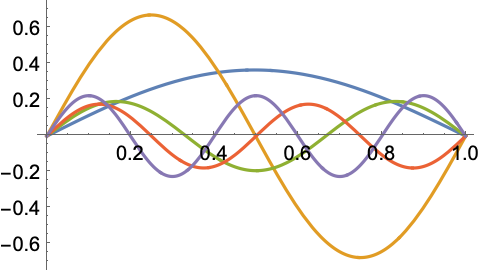
関数 ![]() の固有関数展開中の最初の3項を,区間
の固有関数展開中の最初の3項を,区間![]() 上のディリクレ条件で,1Dラプラス演算子によって与えられた底について計算する:
上のディリクレ条件で,1Dラプラス演算子によって与えられた底について計算する:
https://wolfram.com/xid/0btnz7gc2iv2-chgfue
https://wolfram.com/xid/0btnz7gc2iv2-euk8i9
https://wolfram.com/xid/0btnz7gc2iv2-d8ezwq
https://wolfram.com/xid/0btnz7gc2iv2-khjz1n
https://wolfram.com/xid/0btnz7gc2iv2-byveyd
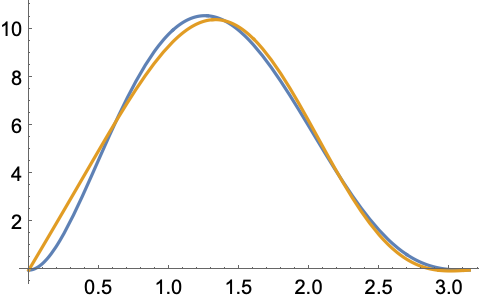
ディリクレ条件を持つ熱伝導方程式について,固有関数の線形結合を用いて解を構築する:
https://wolfram.com/xid/0btnz7gc2iv2-ee0l91
https://wolfram.com/xid/0btnz7gc2iv2-qsijm
https://wolfram.com/xid/0btnz7gc2iv2-q3w8c
https://wolfram.com/xid/0btnz7gc2iv2-h2j74j
https://wolfram.com/xid/0btnz7gc2iv2-bjjefv
https://wolfram.com/xid/0btnz7gc2iv2-d3v70g
CO分子を実質的なバネ定数が ![]() の平衡長の周囲で実験的に振動させる.振動は量子調和振動子方程式によって支配されている.以下では,
の平衡長の周囲で実験的に振動させる.振動は量子調和振動子方程式によって支配されている.以下では,![]() は分子の換算質量,
は分子の換算質量,![]() は固有振動数,
は固有振動数,![]() は平衡位置からの移動,
は平衡位置からの移動,![]() は換算プランク(Planck)定数である:
は換算プランク(Planck)定数である:
https://wolfram.com/xid/0btnz7gc2iv2-551rrk
固有値(それぞれの状態のエネルギー)と正規化された固有関数を計算する:
https://wolfram.com/xid/0btnz7gc2iv2-jxv26o
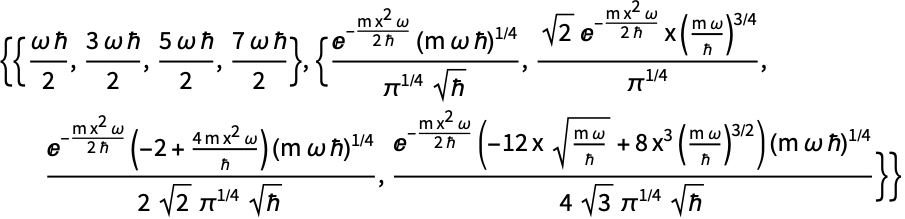
粒子が4状態を等しく重ね合せたものであるなら,波動関数は次の形になる:
https://wolfram.com/xid/0btnz7gc2iv2-qvnvu
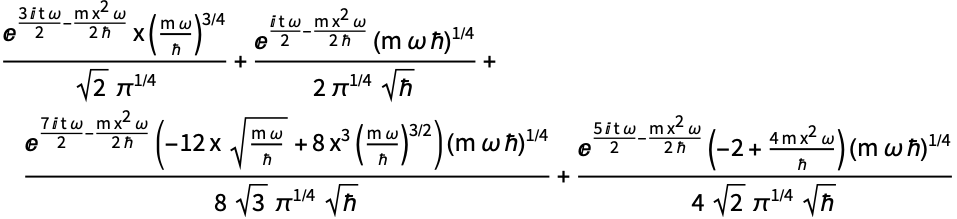
1のオーダーに近い値を与える原子質量単位の基本単位,フェムト秒,ピコメートルを使って ![]() ,
,![]() ,
,![]() を計算する:
を計算する:
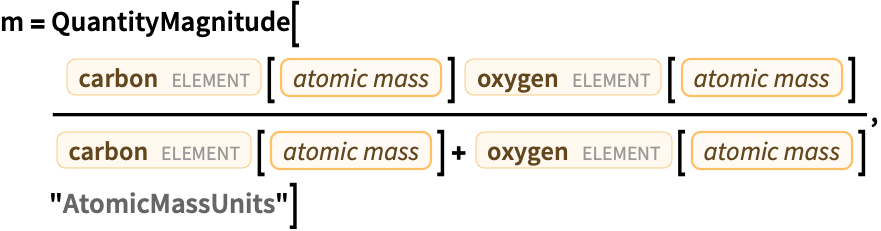
https://wolfram.com/xid/0btnz7gc2iv2-oz2boj
https://wolfram.com/xid/0btnz7gc2iv2-nbi4dx
https://wolfram.com/xid/0btnz7gc2iv2-9qfa20
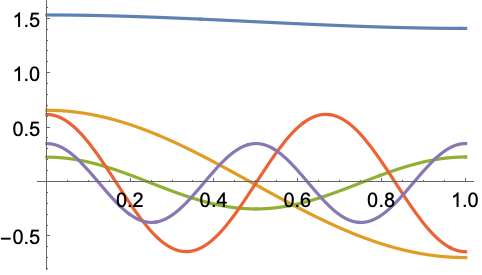
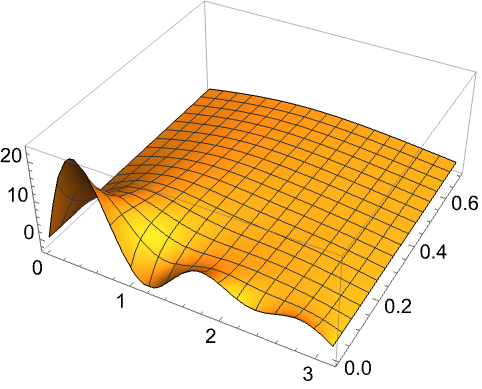
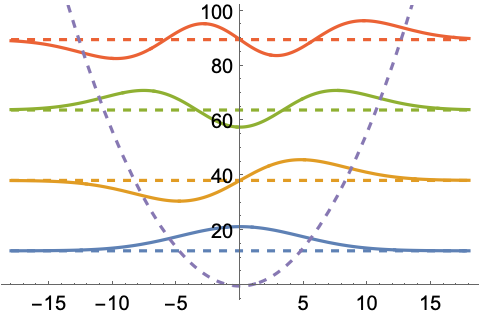
固有関数の位置エネルギー![]() に対する応答は,
に対する応答は,![]() の幅に入るように再スケールすることで可視化できる:
の幅に入るように再スケールすることで可視化できる:
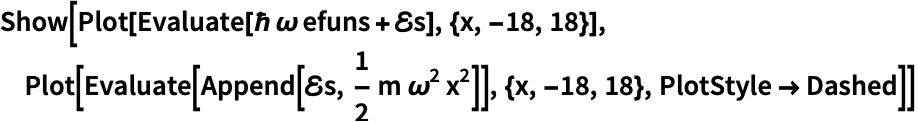
https://wolfram.com/xid/0btnz7gc2iv2-rxoenq
https://wolfram.com/xid/0btnz7gc2iv2-mwva1k

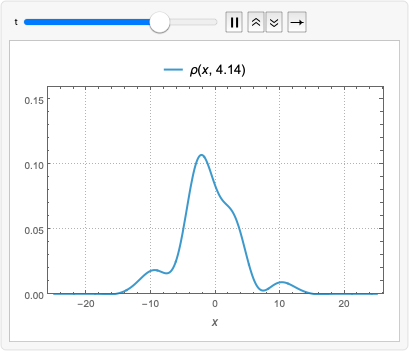
確率分布として,実数上での ![]() の積分はすべての
の積分はすべての ![]() に対して1である:
に対して1である:
https://wolfram.com/xid/0btnz7gc2iv2-cqpldr

https://wolfram.com/xid/0btnz7gc2iv2-s7tsiv
特性と関係 (6)この関数の特性および他の関数との関係
NDEigensystemを使って数値による固有値と固有ベクトルを求める:
https://wolfram.com/xid/0btnz7gc2iv2-b2g6ab
https://wolfram.com/xid/0btnz7gc2iv2-h80wjy
https://wolfram.com/xid/0btnz7gc2iv2-bnu8sm
https://wolfram.com/xid/0btnz7gc2iv2-fub3ug
DEigenvaluesを使って微分演算子についての固有値を求める:
https://wolfram.com/xid/0btnz7gc2iv2-ls3dpn
https://wolfram.com/xid/0btnz7gc2iv2-efw01u
https://wolfram.com/xid/0btnz7gc2iv2-gdvfkv
https://wolfram.com/xid/0btnz7gc2iv2-cb55dh
DSolveを使って固有値問題を解く:
https://wolfram.com/xid/0btnz7gc2iv2-hoe9ag
https://wolfram.com/xid/0btnz7gc2iv2-bqrzjm
https://wolfram.com/xid/0btnz7gc2iv2-es16mg
DEigensystemによって与えられる固有関数は直交関数である:
https://wolfram.com/xid/0btnz7gc2iv2-bbit9o
https://wolfram.com/xid/0btnz7gc2iv2-i15m9d
https://wolfram.com/xid/0btnz7gc2iv2-dfszts
DEigensystemによって与えられる固有関数の系は,デフォルトで,直交系ではない:
https://wolfram.com/xid/0btnz7gc2iv2-gx3hrl
https://wolfram.com/xid/0btnz7gc2iv2-uv309
https://wolfram.com/xid/0btnz7gc2iv2-kwuivh
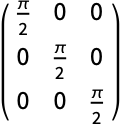
Method->"Normalize"を使って正規直交系を得る:
https://wolfram.com/xid/0btnz7gc2iv2-gzxmv
https://wolfram.com/xid/0btnz7gc2iv2-htdmtj
記号評価が失敗した場合は,N[DEigensystem[...]]を適用してNDEigensystemを呼び出す:
https://wolfram.com/xid/0btnz7gc2iv2-ktfv0
https://wolfram.com/xid/0btnz7gc2iv2-logptw
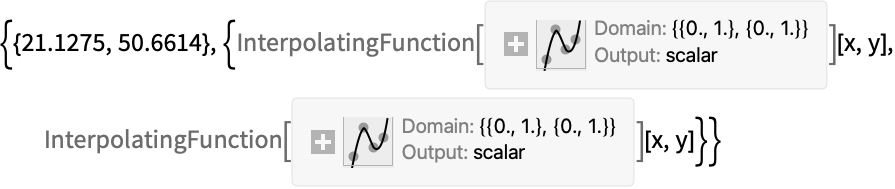
考えられる問題 (2)よく起る問題と予期しない動作
https://wolfram.com/xid/0btnz7gc2iv2-d7hkcu
https://wolfram.com/xid/0btnz7gc2iv2-jg3nz5
https://wolfram.com/xid/0btnz7gc2iv2-vkj213
https://wolfram.com/xid/0btnz7gc2iv2-0cm5i9
Wolfram Research (2015), DEigensystem, Wolfram言語関数, https://reference.wolfram.com/language/ref/DEigensystem.html.テキスト
Wolfram Research (2015), DEigensystem, Wolfram言語関数, https://reference.wolfram.com/language/ref/DEigensystem.html.
Wolfram Research (2015), DEigensystem, Wolfram言語関数, https://reference.wolfram.com/language/ref/DEigensystem.html.CMS
Wolfram Language. 2015. "DEigensystem." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DEigensystem.html.
Wolfram Language. 2015. "DEigensystem." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DEigensystem.html.APA
Wolfram Language. (2015). DEigensystem. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DEigensystem.html
Wolfram Language. (2015). DEigensystem. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DEigensystem.htmlBibTeX
@misc{reference.wolfram_2025_deigensystem, author="Wolfram Research", title="{DEigensystem}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/DEigensystem.html}", note=[Accessed: 13-July-2025
]}BibLaTeX
@online{reference.wolfram_2025_deigensystem, organization={Wolfram Research}, title={DEigensystem}, year={2015}, url={https://reference.wolfram.com/language/ref/DEigensystem.html}, note=[Accessed: 13-July-2025
]}
