DSolveChangeVariables

DSolveChangeVariables[dsolve,u,t,trans]

changes the solution function in dsolve to using the transformation trans.

DSolveChangeVariables[dsolve,{u1,u2,…},t,trans]

changes the solution functions in the system to .

DSolveChangeVariables[dsolve,u,{t1,…,tn},trans]

changes the solution function in the partial differential equation to .

Details and Options

  • A change of variables is often used to simplify the coefficients in a differential expression or to represent it in a more suitable coordinate system such as polar coordinates to exploit the symmetry in the problem.
  • DSolveChangeVariables can be used to perform a change of variables for a single ordinary differential equation or partial differential equation without initial or boundary conditions.
  • The change of variables is performed using the chain rule
  • on an interval 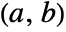or
  • over a region 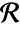where 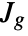denotes the Jacobian of function 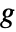with respect to its arguments.
  • The possible forms for dsolve are the forms supported by DSolve:
  • DSolve[deq,y,x]ordinary differential equation
    DSolve[{deq1,…,deqn},{y1,…,yn},x]system of differential equations
    DSolve[deq,z,{x,y,…}]partial differential equation
  • Either an unevaluated DSolve[…] or Inactive[DSolve][…] can be used. It is important that the dsolve does not evaluate, so the safe method is to use Inactive[DSolve][…], which can be produced through Inactivate[dsolve,DSolve].
  • DSolveChangeVariables returns the result in the form Inactive[DSolve][…]. Use Activate to solve the differential equation in the new coordinates. »
  • The transformation trans can have the forms:
  • t==ϕ[x]replace ϕ[x] by t
    {u==ϕ[x,y,…],v=ψ[x,y,…],…}replace ϕ[x,y,…] by u and ψ[x,y,…] by v, etc.
    chart1chart2named coordinate systems from CoordinateChartData
  • The transformation 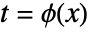is assumed to be differentiable on its domain of definition.
  • When using named coordinate systems, the transformation can be entered in any form accepted by CoordinateTransformData, including {oldsys,metric,dim}{newsys,metric,dim}, {oldsysnewsys,metric,dim} and the various more abbreviated forms.
  • Restrictions on the domains of the variables and parameters in the differential expression can be specified using Assumptions.

Examples

open allclose all

Basic Examples  (4)

Apply the change of variables to a linear differential equation:

Solve the differential equation:

Apply the change of variables to a nonlinear differential equation:

Transform the 2D Laplace equation from Cartesian to the polar coordinate system:

Apply the change of variables to a linear ordinary differential equation:

Solve the resulting differential equation and substitute back to the original variable:

Compare the result with the solution to the original ordinary differential equation:

Scope  (18)

Ordinary Differential Equations  (6)

Simplify a second-order linear differential equation with a change of variables:

Transform the nonlinear Riccati equation to a linear ODE with the change of variables :

Apply the trigonometric transformation to an ordinary differential equation:

Apply the complex-valued transformation and to an ordinary differential equation:

Apply the change of variables to a differential equation:

Reduce a variable-coefficient nonlinear ODE to a constant-coefficient equation using :

Partial Differential Equations  (5)

Transform the -dimensional wave equation into null coordinates:

Apply the same transformation but express the old coordinates in terms of the new ones:

Apply the change of variables to the heat equation:

Apply the change of variables and to a partial differential equation:

Apply the change of variables and to a partial differential equation:

Make a purely symbolic transformation to a partial differential equation:

Partial Differential Equations and Named Coordinate Systems  (7)

Transform a 3D Poisson's equation from Cartesian to the cylindrical coordinate system:

Transform the 3D wave equation from Cartesian to the cylindrical coordinate system:

Transform the 3D biharmonic equation from Cartesian to the spherical coordinate system:

Transform the 3D heat equation in spherical coordinates back to the Cartesian coordinates:

Transform a three-dimensional Schrödinger in spherical coordinates to cylindrical coordinates:

Express the 4D Laplace equation in hyperspherical coordinates:

Transform Poisson's equation on the sphere from standard angular to stereographic coordinates:

Applications  (6)

In quantum mechanics, the operator is a multiple of the angular momentum in the direction. Show this by transforming the equation to polar coordinates:

Consider the Cauchy–Euler equation . It is possible to transform this ODE into an equation with constant coefficients by applying the change of variables :

Apply the transformation to the linear second-order ordinary differential equation :

Dividing the transformed equation by leads to a drastically simplified differential equation:

A spherically symmetric solution to the heat equation (partialf)/(partialt)=TemplateBox[{f, }, Laplacian] in three dimensions can be reduced to a linear ODE. First, write out the equation in spherical coordinates:

Then change to a function of a single variable that combines both space and time coordinates:

In the heat-mass transfer problem, an equation takes the form TemplateBox[{H, }, Laplacian]=u (((1-mu^2) )/r(partialH(r,mu))/(partialmu)+mu (partialH(r,mu))/(partialr)), where is a constant, is the distance from the origin, and is a modification of the polar angle. Starting from standard spherical coordinates, express this equation in local coordinates, then show it can be reduced to Poisson's equation. Set TemplateBox[{H, }, Laplacian] equal to a constant and use DSolveChangeVariables to change how the polar angle is expressed:

Create an operator to express the Laplacian in these coordinates:

Change to new independent variable using :

Divide out the exponential and isolate the term free of the derivatives on the right-hand side:

The left-hand side is the Laplacian in modified spherical coordinates, confirming this is Poisson's equation:

Apply the separation of variables transformation to a Heat equation–type partial differential equation:

After dividing by , you can see that the variables are separated:

Properties & Relations  (2)

A result always has an inactive head, irrespective of the form of input:

DSolveChangeVariables effectively uses the "Mapping" property of CoordinateTransformData:

Possible Issues  (1)

DSolveChangeVariables transforms differential operators, here giving :

Linear differential operators can be transformed as vector fields, though TransformedField will express the result in terms of orthonormal bases, here giving :

Wolfram Research (2022), DSolveChangeVariables, Wolfram Language function, https://reference.wolfram.com/language/ref/DSolveChangeVariables.html.

Text

Wolfram Research (2022), DSolveChangeVariables, Wolfram Language function, https://reference.wolfram.com/language/ref/DSolveChangeVariables.html.

CMS

Wolfram Language. 2022. "DSolveChangeVariables." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DSolveChangeVariables.html.

APA

Wolfram Language. (2022). DSolveChangeVariables. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DSolveChangeVariables.html

BibTeX

@misc{reference.wolfram_2023_dsolvechangevariables, author="Wolfram Research", title="{DSolveChangeVariables}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/DSolveChangeVariables.html}", note=[Accessed: 19-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2023_dsolvechangevariables, organization={Wolfram Research}, title={DSolveChangeVariables}, year={2022}, url={https://reference.wolfram.com/language/ref/DSolveChangeVariables.html}, note=[Accessed: 19-April-2024 ]}