DSolveChangeVariables

DSolveChangeVariables[dsolve,u,t,trans]

変換 trans を使って dsolve の解の関数を に変える．

DSolveChangeVariables[dsolve,{u1,u2,…},t,trans]

系の解の関数をに変える．

DSolveChangeVariables[dsolve,u,{t1,…,tn},trans]

偏微分方程式の解の関数を に変える．

詳細とオプション

  • 変数の変更は微分方程式における係数を簡約するため，あるいは問題の対称性を利用するために微分方程式をより適切な極座標で表すためにしばしば用いられる．
  • DSolveChangeVariablesを使って，単一の常微分方程式あるいは初期条件または境界条件がない偏微分方程式の変数が変更できる．
  • 変数の変更は以下の連鎖律を
  • 区間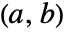上，あるいは
  • 領域 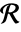上で使って実行できる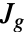．は関数 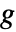のその引数についてのヤコビアンを示す．
  • dsolve の可能な形はDSolveがサポートする形である．
  • DSolve[deq,y,x]常微分方程式
    DSolve[{deq1,…,deqn},{y1,…,yn},x]微分方程式系
    DSolve[deq,z,{x,y,…}]偏微分方程式
  • 未評価のDSolve[…]あるいはInactive[DSolve][…]を使うことができる．dsolve を評価しないことが重要なので，Inactivate[dsolve,DSolve]で生成されるInactive[DSolve][…]を使うとよいだろう．
  • DSolveChangeVariablesは結果をInactive[DSolve][…]の形で返す．Activateを使って新たな座標で微分方程式を解く． »
  • 変換 trans には次の形がある．
  • t==ϕ[x]ϕ[x]を t で置換する
    {u==ϕ[x,y,…],v=ψ[x,y,…],…}ϕ[x,y,…]を u で，ψ[x,y,…]を v で置換する等
    chart1chart2CoordinateChartDataからの名前付き座標系
  • 変換 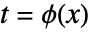はその定義域上で微分可能であると仮定される．
  • 名前付きの座標系を使う際は，{oldsys,metric,dim}{newsys,metric,dim}，{oldsysnewsys,metric,dim}，および，より省略されたさまざまな形式を含むCoordinateTransformDataが取る任意の形で変換を入力することができる．
  • 微分方程式の変数とパラメータの領域はAssumptionsを使って制限できる．

例題

すべて開くすべて閉じる

例  (4)

線形微分方程式に変数の変更 を適用する：

微分方程式を解く：

非線形微分方程式に変数の変更 を適用する：

2Dラプラス方程式を直交座標系から極座標系に変換する：

変数の変更 を線形常微分方程式に適用する：

結果の微分方程式を解いてもとの変数に代入し直す：

結果をもとの常微分方程式の解と比較する：

スコープ  (18)

常微分方程式  (6)

変数を変更して二階線形微分方程式を簡約する：

変数 を変更して線形リッカティ(Riccati)方程式を常微分方程式に変換する：

常微分方程式に三角変換 を適用する：

常微分方程式に複素数値変換 と を適用する：

微分方程式に変数の変更 を適用する：

を次使って変数係数を持つ非線形常微分方程式を定数係数を持つ方程式に簡約する：

偏微分方程式  (5)

次元波動方程式をヌル座標に変換する：

同じ変換を適用するが，もとの座標を新たな座標を使って表す：

変数の変更 を熱方程式に適用する：

変数の変更 および を偏微分方程式に適用する：

変数の変更 と を偏微分方程式に適用する：

偏微分方程式に純粋に記号的な変換を適用する：

偏微分方程式と名前付きの座標系  (7)

3Dポアソン(Poisson)方程式を直交座標系から円柱座標系に変換する：

3D波動方程式を直交座標系から円柱座標系に変換する：

3D重調和方程式を直交座標系から球座標系に変換する：

3D熱伝導方程式を球座標系から直交座標系に変換し直す：

3Dシュレディンガー(Schrödinger)方程式を球座標系から円柱座標系に変換する：

4Dラプラス方程式を超球座標で表す：

球上のポアソン方程式を標準角座標から立体座標に変換する：

アプリケーション  (6)

量子力学では，演算子 は 方向の角運動量の倍数である．方程式 を極座標に変換することでこれを示す：

コーシー・オイラー(Cauchy–Euler)方程式 について考える．変数の変更 を適用することで，この常微分方程式を定係数を持つ方程式に変換することができる：

二階線形常微分方程式 に変形 を適用する：

変形された方程式をで割ると大幅に簡約された微分方程式になる：

三次元熱方程式(partialf)/(partialt)=TemplateBox[{f, }, Laplacian] の球対称解は線形常微分方程式に簡約できる．まず，方程式を球座標で書く：

次に空間座標と時間座標の両方を組み合せる特異値 の関数に変形する：

熱物質移動問題の方程式はTemplateBox[{H, }, Laplacian]=u (((1-mu^2) )/r(partialH(r,mu))/(partialmu)+mu (partialH(r,mu))/(partialr))という形になる．ここで， は定数， は原点からの距離，は極角の修正である．標準的な球座標から始めて，この方程式を局所座標で表し次にこれがポアソン(Poisson)方程式に簡約できることを示す．TemplateBox[{H, }, Laplacian] が定数と等しいとし，DSolveChangeVariablesを使って極座標の表し方を変える：

これらの座標でラプラシアンを表す演算子を作成する：

を使って新たな独立変数に変更する：

指数を割り，右辺の導関数を含まない項を分離する：

左辺は修正された球座標におけるラプラシアンで，これがポアソン方程式であることが確認できる：

熱方程式型の偏微分方程式に変数の分離変換を適用する：

で割った後で変数が分離されているのが分かる：

特性と関係  (2)

結果は入力の形と関係なく常に不活性な頭部を持つ：

DSolveChangeVariablesは，事実上，CoordinateTransformDataの"Mapping"特性を使う：

考えられる問題  (1)

DSolveChangeVariablesは微分演算子を変換し，ここではを与えている：

TransformedFieldは結果を正規直交基底で表し，ここではを与えているが，線形微分演算子はベクトル場として変換できる：

Wolfram Research (2022), DSolveChangeVariables, Wolfram言語関数， https://reference.wolfram.com/language/ref/DSolveChangeVariables.html.

テキスト

Wolfram Research (2022), DSolveChangeVariables, Wolfram言語関数， https://reference.wolfram.com/language/ref/DSolveChangeVariables.html.

CMS

Wolfram Language. 2022. "DSolveChangeVariables." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DSolveChangeVariables.html.

APA

Wolfram Language. (2022). DSolveChangeVariables. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DSolveChangeVariables.html

BibTeX

@misc{reference.wolfram_2024_dsolvechangevariables, author="Wolfram Research", title="{DSolveChangeVariables}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/DSolveChangeVariables.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_dsolvechangevariables, organization={Wolfram Research}, title={DSolveChangeVariables}, year={2022}, url={https://reference.wolfram.com/language/ref/DSolveChangeVariables.html}, note=[Accessed: 22-November-2024 ]}