represents a Daubechies wavelet of order 2.
represents a Daubechies wavelet of order n.


DaubechiesWavelet
represents a Daubechies wavelet of order 2.
represents a Daubechies wavelet of order n.
Details
- DaubechiesWavelet defines a family of orthogonal wavelets.
- DaubechiesWavelet[n] is defined for any positive integer n.
- The scaling function (
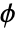 ) and wavelet function (
) and wavelet function (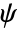 ) have compact support length of 2n. The scaling function has n vanishing moments.
) have compact support length of 2n. The scaling function has n vanishing moments. - DaubechiesWavelet can be used with such functions as DiscreteWaveletTransform, WaveletPhi, etc.
Examples
open all close allScope (14)
Basic Uses (8)
Compute primal lowpass filter coefficients:
Primal highpass filter coefficients:
Generate a function to compute a lifting wavelet transform:
Daubechies scaling function of order 2:
Daubechies scaling function of order 6:
Plot scaling function using different levels of recursion:
Daubechies wavelet function of order 2:
DaubechiesWavelet of order 6:
Wavelet Transforms (5)
Compute a DiscreteWaveletTransform:
View the tree of wavelet coefficients:
Get the dimensions of wavelet coefficients:
Plot the wavelet coefficients:
Compute a DiscreteWaveletPacketTransform:
View the tree of wavelet coefficients:
Get the dimensions of wavelet coefficients:
Plot the wavelet coefficients:
Compute a StationaryWaveletTransform:
View the tree of wavelet coefficients:
Get the dimensions of wavelet coefficients:
Plot the wavelet coefficients:
Compute a StationaryWaveletPacketTransform:
View the tree of wavelet coefficients:
Get the dimensions of wavelet coefficients:
Plot the wavelet coefficients:
Compute a LiftingWaveletTransform:
View the tree of wavelet coefficients:
Applications (3)
Approximate a function using Daubechies wavelet coefficients:
Perform a LiftingWaveletTransform:
Approximate original data by keeping n largest coefficients and thresholding everything else:
Compare the different approximations:
Compute the multiresolution representation of a signal containing an impulse:
Compare the cumulative energy in a signal and its wavelet coefficients:
Compute the ordered cumulative energy in the signal:
The energy in the signal is captured by relatively few wavelet coefficients:
Properties & Relations (13)
DaubechiesWavelet[1] is equivalent to HaarWavelet:
Lowpass filter coefficients sum to unity; ![]() :
:
Highpass filter coefficients sum to zero; ![]() :
:
Scaling function integrates to unity; ![]() :
:
Wavelet function integrates to zero; ![]() :
:
Wavelet function is orthogonal to the scaling function at the same scale; ![]() :
:
The lowpass and highpass filter coefficients are orthogonal; ![]() :
:
DaubechiesWavelet[n] has n vanishing moment; ![]() :
:
This means linear signals are fully represented in the scaling functions part ({0}):
Quadratic or higher-order signals are not:
![]() satisfies the recursion equation
satisfies the recursion equation ![]() :
:
Plot the components and the sum of the recursion:
![]() satisfies the recursion equation
satisfies the recursion equation ![]() :
:
Plot the components and the sum of the recursion:
Frequency response for ![]() is given by
is given by ![]() :
:
The filter is a lowpass filter:
The higher the order n, the flatter the response function at the ends:
Fourier transform of ![]() is given by
is given by ![]() :
:
Frequency response for ![]() is given by
is given by ![]() :
:
The filter is a highpass filter:
The higher the order n, the flatter the response function at the ends:
Tech Notes
Related Guides
History
Text
Wolfram Research (2010), DaubechiesWavelet, Wolfram Language function, https://reference.wolfram.com/language/ref/DaubechiesWavelet.html.
CMS
Wolfram Language. 2010. "DaubechiesWavelet." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DaubechiesWavelet.html.
APA
Wolfram Language. (2010). DaubechiesWavelet. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DaubechiesWavelet.html
BibTeX
@misc{reference.wolfram_2025_daubechieswavelet, author="Wolfram Research", title="{DaubechiesWavelet}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/DaubechiesWavelet.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_daubechieswavelet, organization={Wolfram Research}, title={DaubechiesWavelet}, year={2010}, url={https://reference.wolfram.com/language/ref/DaubechiesWavelet.html}, note=[Accessed: 24-February-2026]}