DesignMatrix

DesignMatrix[{{x11,x12,…,y1},{x21,x22,…,y2},…},{f1,f2,…},{x1,x2,…}]

線形モデル β0+β1 f1+β2 f2+… の計画行列を構築する．

詳細とオプション

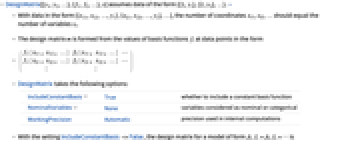
  • DesignMatrix[{y1,y2,…},{f1,f2,…},x]は{{1,y1},{2,y2},…}の形式のデータを想定している． »
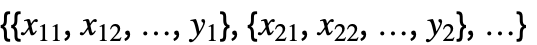  • {{x_(11),x_(12),...,y_(1)},{x_(21),x_(22),...,y_(2)},...}の形のデータのとき，座標 xi1, xi2, …の数は変数 xiの数に等しくなければならない．
  • 計画行列 m は以下の形のデータ点における基底関数 fiの値から形成される．
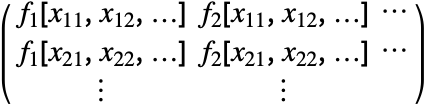
  • DesignMatrixで使用可能なオプション
  • IncludeConstantBasis True定数基底関数を含むかどうか
    NominalVariables None名義的あるいはカテゴリ的とみなされる変数
    WorkingPrecisionAutomatic内部計算で使う精度
  • IncludeConstantBasis->Falseと設定すると，β1 f1+β2 f2+⋯の形式のモデルに対する計画行列が構築される． »

例題

すべて開くすべて閉じる

例  (3)

線形モデルの計画行列：

二次項を加える：

係数項を除外する：

2つの予測変数を持つ計画行列：

積の項を含む：

予測変数1, 2, …を推定する：

スコープ  (2)

予測器の任意の数値関数を使う：

厳密な演算で計画行列を得る：

機械演算を使う：

任意精度演算を使う：

固定24桁精度演算を使う：

オプション  (3)

IncludeConstantBasis  (1)

デフォルトでは定数項が含まれる：

定数項なしで計画行列を構築する：

NominalVariables  (2)

x を数値変数として扱う：

x を名義変数として扱う：

数値的ではない名義変数を使う：

x のみを名義変数として扱う：

すべての予測器を名義変数として扱う：

特性と関係  (1)

DesignMatrixはLinearModelFitで使われる計画行列を構築する：

この行列はGeneralizedLinearModelFitについても同じである：

Wolfram Research (2008), DesignMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/DesignMatrix.html.

テキスト

Wolfram Research (2008), DesignMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/DesignMatrix.html.

CMS

Wolfram Language. 2008. "DesignMatrix." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DesignMatrix.html.

APA

Wolfram Language. (2008). DesignMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DesignMatrix.html

BibTeX

@misc{reference.wolfram_2024_designmatrix, author="Wolfram Research", title="{DesignMatrix}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/DesignMatrix.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_designmatrix, organization={Wolfram Research}, title={DesignMatrix}, year={2008}, url={https://reference.wolfram.com/language/ref/DesignMatrix.html}, note=[Accessed: 22-November-2024 ]}