DifferenceQuotient[f,{x,h}]
gives the difference quotient ![]() .
.
DifferenceQuotient[f,{x,n,h}]
gives a multiple difference quotient with step h.
DifferenceQuotient[f,{x1,n1,h1},{x2,n2,h2},…]
computes the partial difference quotient with respect to x1,x2,….


DifferenceQuotient
DifferenceQuotient[f,{x,h}]
gives the difference quotient ![]() .
.
DifferenceQuotient[f,{x,n,h}]
gives a multiple difference quotient with step h.
DifferenceQuotient[f,{x1,n1,h1},{x2,n2,h2},…]
computes the partial difference quotient with respect to x1,x2,….
Details and Options
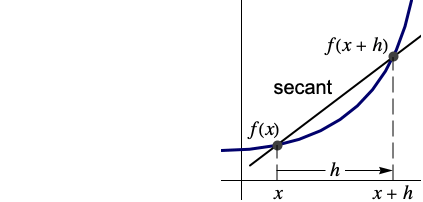
- DifferenceQuotient gives the slope of the secant line joining two nearby points on a curve.
- DifferenceQuotient[f,{x,n,h}] is equivalent to DifferenceDelta[f,{x,n,h}]/
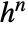 .
. - DifferenceQuotient[f,…,Assumptions->assum] uses the assumptions assum in the course of computing difference quotients.
Examples
open all close allBasic Examples (1)
Scope (16)
Basic Uses (4)
Compute a forward difference quotient with step h:
Symmetric difference quotient:
Compute the second difference quotient with step h:
Partial difference quotient with steps r and s:
DifferenceQuotient threads over lists:
Univariate Difference Quotients (8)
DifferenceQuotient of a constant is 0:
DifferenceQuotient of a polynomial function is a polynomial function:
Each successive difference quotient will lower the degree in x by one:
Difference quotients of rational functions will stay as rational functions:
Difference quotients of PolyGamma with an integer step are rational functions:
Similarly for HarmonicNumber and Zeta:
FactorialPower with step h has a simple difference quotient for a matching step h:
Multivariate Difference Quotients (4)
DifferenceQuotient of a multivariate polynomial function is a polynomial function:
Difference quotients of multivariate rational functions will stay as rational functions:
Higher-order quotients will tend to grow in size:
DifferenceQuotient of multivariate functions depending on a subset of the variables are 0:
DifferenceQuotient for a product of univariate functions:
This is equal to the product of the individual difference quotients:
Options (1)
Applications (10)
Derivatives from First Principles (3)
Compute the derivative of a polynomial from first principles:
Compute the derivative using D:
Compute the second derivative for a power function:
Third derivative for a power tower:
Compute the partial derivative with respect to x for a function of two variables:
Approximate Derivatives (3)
Approximate the derivative at a point using DifferenceQuotient:
Approximation given by DifferenceQuotient:
Approximate the derivative of a function using various difference quotients:
Use forward difference quotients to obtain an approximation:
Backward difference quotients:
Symmetric difference quotients:
Approximate the partial derivatives at a point using DifferenceQuotient:
Differential Equations (3)
Discretize a differential equation using forward differences:
Solve the differential equation using DSolveValue:
Solve the difference equation using RSolveValue:
Compare the exact and approximate solutions:
Discretize a differential equation using backward differences:
Solve the differential equation using DSolveValue:
Solve the difference equation using RSolveValue:
Compare the exact and approximate solutions:
Discretize a differential equation using symbolic differences:
Solve the differential equation using DSolveValue:
Solve the difference equation using RSolveValue:
Compare the exact and approximate solutions using forward and backward differences:
Obtain the exact solution as a limit of the approximate solution:
Extrapolation (1)
Richardson extrapolation is a method for sequence acceleration that can be used to improve the rate of convergence of a sequence a[h], which depends on a parameter h. Apply Richardson extrapolation to accelerate the convergence of DifferenceQuotient to the derivative of a function f[x] using the sequence a[x,h], which is defined by:
Set up a scheme for Richardson extrapolation:
Compute the derivative at a point:
Approximation given by DifferenceQuotient:
Richardson extrapolation improves the derivative approximation:
Properties & Relations (6)
DifferenceQuotient gives the slope of the secant line joining two nearby points on a curve:
The Limit of DifferenceQuotient is the derivative D:
An iterated Limit of a multiple difference quotient gives a mixed partial derivative:
DifferenceQuotient is related to DifferenceDelta as ![]() :
:
DifferenceQuotient is related to DiscreteShift as ![]() :
:
DifferenceQuotient is a linear operator:
Interactive Examples (1)
See Also
DifferenceDelta D DiscreteShift DiscreteRatio Differences ReplaceAll
Function Repository: PolynomialDividedDifference FiniteDifferenceStencil
Related Guides
History
Text
Wolfram Research (2016), DifferenceQuotient, Wolfram Language function, https://reference.wolfram.com/language/ref/DifferenceQuotient.html.
CMS
Wolfram Language. 2016. "DifferenceQuotient." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DifferenceQuotient.html.
APA
Wolfram Language. (2016). DifferenceQuotient. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DifferenceQuotient.html
BibTeX
@misc{reference.wolfram_2025_differencequotient, author="Wolfram Research", title="{DifferenceQuotient}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/DifferenceQuotient.html}", note=[Accessed: 06-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_differencequotient, organization={Wolfram Research}, title={DifferenceQuotient}, year={2016}, url={https://reference.wolfram.com/language/ref/DifferenceQuotient.html}, note=[Accessed: 06-January-2026]}